Cho \(\Delta\)ABC,các đường trung tuyến AM,BE,CF cắt nhau tại G
a)Chứng minh:S\(\Delta\)BAG=\(\dfrac{1}{3}\)S\(\Delta\)ABC
b)Chứng minh S\(\Delta\)ABG=S\(\Delta\)ACG=S\(\Delta\)BCG
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2022
a: Xét ΔAEI vuông tại E và ΔBHI vuông tại H có
góc AIE=góc BIH
Do đó: ΔAEI đồng dạng vớiΔBHI
c: Sửa đề: \(BA\cdot BF+CE\cdot CA=BC^2\)
Xét ΔBFC vuông tại F và ΔBHA vuông tại H có
góc FBC chung
Do đó;ΔBFC\(\sim\)ΔBHA
Suy ra: BF/BH=BC/BA
hay \(BF\cdot BA=BH\cdot BC\)
Xét ΔCEB vuông tại E và ΔCHA vuông tại H có
góc HCA chung
Do đo ΔCEB\(\sim\)ΔCHA
Suy ra: CE/CH=CB/CA
hay \(CA\cdot CE=CH\cdot CB\)
=>\(BA\cdot BF+CA\cdot CE=BC^2\)
5 tháng 2 2020
a)Xét đồng dạng ms đc, bằng nhua cái kiểu j
Xét ABM và ACN có góc A chung góc N=M=90
5 tháng 2 2020
b/Từ 2 tam giác đồng dạng bằng nhau ở a➩AN/AC=AM/AB,Lại có góc A chung nên suy ra AMN đồng dạng ABC
SN
0
31 tháng 7 2023
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
=>ΔABH=ΔACH
b: Xét ΔACB có
BM,AH là trung tuyến
BM cắt AH tại G
=>G là trọng tâm
=>C,G,N thẳng hàng
c: Xét ΔABG và ΔACG có
AB=AC
góc BAG=góc CAG
AG chung
=>ΔABG=ΔACG
AH
Akai Haruma
Giáo viên
9 tháng 5 2018
Lời giải:
a)
Xét tam giác $CFB$ và $ADB$ có:
\( \left\{\begin{matrix} \widehat{CFB}=\widehat{ADB}=90^0\\ \text{chung góc B}\end{matrix}\right.\Rightarrow \triangle CFB\sim \triangle ADB(g.g) \)
b)
Xét tam giác $AFH$ và $ADB$ có:
\( \left\{\begin{matrix} \widehat{AFH}=\widehat{ADB}=90^0\\ \text{chung góc A}\end{matrix}\right.\Rightarrow \triangle AFH\sim \triangle ADB(g.g)\)
\(\Rightarrow \frac{AF}{AD}=\frac{AH}{AB}\Rightarrow AF.AB=AD.AH\)
c)
Xét tam giác $ABD$ và $CBF$ có:
\( \left\{\begin{matrix} \widehat{ADB}=\widehat{CFB}\\ \text{chung góc B}\end{matrix}\right.\Rightarrow \triangle ABD\sim \triangle CBF(g.g)\)
\(\Rightarrow \frac{AB}{CB}=\frac{BD}{BF}\)
Xét tam giác $BDF$ và $BAC$ có:
\( \left\{\begin{matrix} \text{chung góc B}\\ \frac{BD}{BF}=\frac{BA}{BC}(cmt)\end{matrix}\right.\Rightarrow \triangle BDF\sim \triangle BAC(c.g.c)\)
d) Đề sai hiển nhiên.
28 tháng 4 2020
a) Ta có: ΔABC cân tại A(gt)
⇒\(\widehat{ACB}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔABC cân tại A)
hay \(\widehat{ACB}=\frac{180^0-40^0}{2}=70^0\)
Xét ΔABC có
\(\widehat{ACB}>\widehat{BAC}\left(70^0>40^0\right)\)
mà cạnh đối diện với \(\widehat{ACB}\) là AB
và cạnh đối diện với \(\widehat{BAC}\) là BC
nên AB>BC(Định lí 2 về quan hệ giữa góc và cạnh trong tam giác)
b) Xét ΔADB và ΔADC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD là cạnh chung
Do đó: ΔADB=ΔADC(c-g-c)
c) Ta có: ΔADB=ΔADC(cmt)
⇒DB=DC(hai cạnh tương ứng)
mà B,D,C thẳng hàng
nên D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(D là trung điểm của BC)
BE là đường trung tuyến ứng với cạnh AC(gt)
\(AD\cap BE=\left\{H\right\}\)
Do đó: H là trọng tâm của ΔABC(tính chất ba đường trung tuyến của tam giác)
hay CH đi qua trung điểm của cạnh AB(đpcm)
d) Ta có: \(\widehat{ABC}+\widehat{KBC}=\widehat{ABK}=90^0\)(tia BC nằm giữa hai tia BA,BK)
\(\widehat{ACB}+\widehat{KCB}=\widehat{ACK}=90^0\)(tia CB nằm giữa hai tia CA,CK)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{KBC}=\widehat{KCB}\)
Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)(cmt)
nên ΔKBC cân tại K(định lí đảo của tam giác cân)
⇔KB=KC
hay K nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: BD=CD(cmt)
nên D nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(3)
Từ (1), (2) và (3) suy ra A,D,K thẳng hàng(đpcm)
14 tháng 9 2023
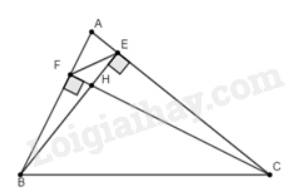
a) Vì \(BE\)là đường cao nên \(\widehat {AEB} = 90^\circ \); vì \(CF\)là đường cao nên \(\widehat {AFC} = 90^\circ \)
Xét tam giác \(AEB\) và tam giác \(AFC\) có:
\(\widehat A\) (chung)
\(\widehat {AEB} = \widehat {AFC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AEB\backsim\Delta AFC\) (g.g).
b) Vì \(\Delta AEB\backsim\Delta AFC\) nên \(\widehat {ACF} = \widehat {ABE}\) (hai góc tương ứng) hay \(\widehat {ECH} = \widehat {FBH}\).
Xét tam giác \(HEC\) và tam giác \(HFB\) có:
\(\widehat {ECH} = \widehat {FBH}\) (chứng minh trên)
\(\widehat {CEH} = \widehat {BFH} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HEC\backsim\Delta HFC\) (g.g).
Suy ra, \(\frac{{HE}}{{HF}} = \frac{{HC}}{{HB}}\) (các cặp cạnh tương ứng tỉ lệ)
Hay \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (điều phải chứng minh).
c) Xét tam giác \(HEF\) và tam giác \(HCB\) có:
\(\widehat {FHE} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (chứng minh trên)
Suy ra, \(\Delta HEF\backsim\Delta HCB\) (c.g.c).
17 tháng 9 2023
a) G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC.
Suy ra: \(AG = 2GM\). Mà trên tia đối của tia MA lấy điểm D sao cho MD = MG nên \(GD = 2GM\).
Vậy GA = GD (= 2GM).
b) Xét hai tam giác MBG và MCD có:
MB = MC (M là trung điểm cạnh BC)
\(\widehat {GMB} = \widehat {DMC}\)(đối đỉnh)
GM = GD.
Vậy \(\Delta MBG = \Delta MCD\)(c.g.c).
c) \(\Delta MBG = \Delta MCD\) nên BG = CD (2 cạnh tương ứng).
Mà G là trọng tâm tam giác ABC nên \(BG = 2GN\). Mà BG = CD nên \(CD = 2GN\).