Có 2 người đi với vận tốc k đổi. Nếu chuyển động cùng chiều thì sau mỗi giờ khoảng giữa 2 người tăng thêm 10km. Nếu chuyển động ngược chiều thì chỉ cần 12 phút khoảng cách giữa 2 người giảm 10km. Tìm v1 và v2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
20 tháng 2 2019
Chọn đáp án C
Gọi vận tốc của hai xe lần lượt là v 1 , v 2
Khi hai xe chuyển động ngược chiều thì
Khi hai xe chuyển động cùng chiều thì
11 tháng 7 2017
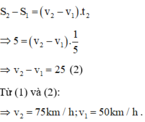
Gọi v1; v2 lần lượt là vận tốc 2 xe.
s1; s2 lần lượt là quãng đường 2 xe đi được trong 2 trường hợp.
Theo bài ra ta có:
\(s_1=\left(v_1+v_2\right)t=25\Rightarrow v_1+v_2=\dfrac{25}{0,25}=100\left(\text{km/h}\right)\left(1\right)\)
Giả sử v1 > v2:
\(s_2=\left(v_1-v_2\right)t=5\Rightarrow v_1-v_2=\dfrac{5}{0,25}=20\left(\text{km/h}\right)\left(2\right)\)
Lấy (1)+(2); ta có: \(2v_1=120\Rightarrow v_1=60\left(\text{km/h}\right)\Rightarrow v_2=40\left(\text{km/h}\right)\)
Vậy......................
13 tháng 1 2022
Vận tốc của mỗi vật là:
\(\begin{cases} v_1+v_2=\dfrac{s_1}{t_1}<=> v_1+v_2=\dfrac{16}{12}=\dfrac{4}{3}\\ v_1-v_2=\dfrac{s_2}{t_2}<=> v_1-v_2=\dfrac{6}{12,5}=0,48 \end{cases} \)
\(=> \begin{cases} v_1=0,9m/s\\ v_2=0,42m/s \end{cases} \)
Quãng đường 2 vật đi được sau 45s là:
\(s_1'=v_1t=0,9.45=40,5(m)\)
\(s_2'=v_2t=0,42.45=18,9(m)\)
KH
1 tháng 7 2017
Hai xe chuyển động thẳng đều trên cùng một đường thẳng. Nếu đi ngược chiều thì sau 15 phút, khoảng cách giữa hai xe giảm 25km. Nếu đi cùng chiều thì sau 15 phút khỏng cách giữa hai xe chỉ giảm 5km. Tính vận tốc của mỗi xe.
Chọn chiều dương là chiều chuyển động của mỗi xe. Quãng đường mỗi xe đi được trong thời gian t: s1= v1.t ; s2 = v2.t
Khi đi ngược chiều, tổng quãng đường hai xe đi được chính là độ giảm khoảng cách:
s1 + s2 = (v1 + v2)t ⇒ \(\dfrac{v_1+v_2}{3}=25\) (1) Khi đi cùng chiều, hiệu quãng đường hai xe đi được chính là độ giảm về khoảng cách:
s2 − s1 = (v2 − v1)t ⇒ \(\dfrac{v_2-v_1}{3}=5\) (2) Từ (1) và (2) ta có hệ phương trình : \(\left\{{}\begin{matrix}v_1+v_2=25\\v_2-v_1=18\end{matrix}\right.\) Suy ra: v1 = 36 km/h ; v2 = 54 km/h. P/s: về phần này t chưa nắm kĩ rõ cho lém nên hỏi vài người này đê. @Như Khương Nguyễn, @Kayoko,. . . .
s1 + s2 = (v1 + v2)t ⇒ \(\dfrac{v_1+v_2}{3}=25\) (1) Khi đi cùng chiều, hiệu quãng đường hai xe đi được chính là độ giảm về khoảng cách:
s2 − s1 = (v2 − v1)t ⇒ \(\dfrac{v_2-v_1}{3}=5\) (2) Từ (1) và (2) ta có hệ phương trình : \(\left\{{}\begin{matrix}v_1+v_2=25\\v_2-v_1=18\end{matrix}\right.\) Suy ra: v1 = 36 km/h ; v2 = 54 km/h. P/s: về phần này t chưa nắm kĩ rõ cho lém nên hỏi vài người này đê. @Như Khương Nguyễn, @Kayoko,. . . .
KA
4 tháng 9 2017
Đổi 15 phút=1/4 h
Khi đi ngược chiều trong 15 phút tổng quãng đường 2 xe đi được là:
S1=1/4.(v1+v2)=25
=>v1+v2=100(km) (1)
Khi đi cùng chiều trong 15 phút khi đó khoảng cách giữa hai xe giảm 5km nên ta có:
1/4.(v1-v2)=5
=>v1-v2=20(km) (2)
Từ (1) và (2) giải hệ phương trình được v1=60(km/h) v2=40(km/h)
Đi cùng chiều: \(v_1-v_2=\dfrac{10}{1}=10\)
Đi ngược chiều: \(v_1+v_2=\dfrac{10}{\dfrac{12}{60}}\Rightarrow v_1+v_2=50\)
\(\Rightarrow\left\{{}\begin{matrix}v_1=...\left(km/h\right)\\v_2=...\left(km/h\right)\end{matrix}\right.\)
Mk thấy bạn trả lời nhiều người quá ha