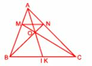
Cho hinh tam giác ABC , gọi M là trung điểm của cạnh BC và N nằm trên cạnh AC sao cho NC = 2 nhân với NA. Kéo dài MN cắt cạnh BA kéo dài tại P.
a , Chứng tỏ rằng AB =AP ?
b , Gọi Q là điểm chính giữa của PC . Chứng tỏ rằng ba điểm B , N , Q cùng năm trêm một đường thẳng ?
c , Hãy so sánh : PN và NM , BN và NQ ?
Ai làm được sẽ được tôi like rất nhiều !

chưa j năm ms thấy tốn giấy quớ olm ơi!