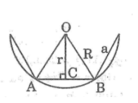
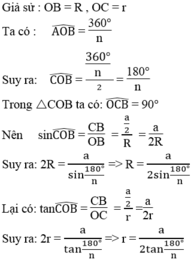
Độ dài bán kính đường tròn nội tiếp của tam giác có ba cạnh là 8; 17 và 15 là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
1
7 tháng 2 2016
Ta có: 82 + 152 = 289 , 172 = 289
=> 82 + 152 = 172
=> tam giác ABC vuông tại A
Tui chỉ bik làm tới đó thui , nếu đề là tính bán kính đường tròn ngoại tiếp thì tui bik lm , còn nội tiếp thì chịu
HQ
1
28 tháng 2 2016
Ap dụng công thức S=p.r (r là bán kính đtron nội tiếp,p là nửa chu vi)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2021
Gọi 3 cạnh tam giác là \(a\) ; \(a+d\) ; \(a+2d\) (với \(a>d\))
\(p=\dfrac{3a+3d}{2}\) ; \(r^2=\dfrac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p}=9\)
\(\Rightarrow\left(\dfrac{a+3d}{2}\right)\left(\dfrac{a+d}{2}\right)\left(\dfrac{a-d}{2}\right)=\dfrac{27}{2}\left(a+d\right)\)
\(\Leftrightarrow\left(a+3d\right)\left(a-d\right)=108\)
Do \(\left(a+3d\right)+\left(a-d\right)=2\left(a+d\right)\) chẵn ta chỉ cần xét các cặp ước dương cùng tính chẵn lẻ của 108
TH1: \(\left\{{}\begin{matrix}a+3d=54\\a-d=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=15\\d=13\end{matrix}\right.\)
Ba cạnh là: \(\left(15;28;41\right)\)
TH2: \(\left\{{}\begin{matrix}a+3d=18\\a-d=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=9\\d=3\end{matrix}\right.\)
Ba cạnh là: \(\left(9;12;15\right)\)
25 tháng 9 2023
Tham khảo:
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
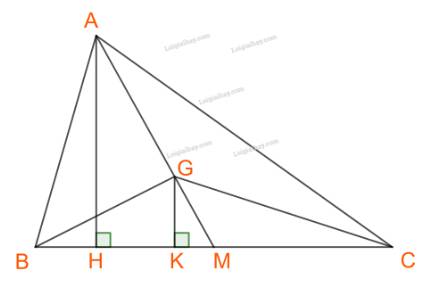
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)
13 tháng 12 2015
ABC vuông tại A
Gọi r là bán kính ; các tiếp điểm AC ;AB ;BC la M;N;P
=> AN = AM =r
=> BN =BP =AB - r = 4- r ; CM =CP =AC-r = 3 -r
Mà BP + PC =BC => 4-r + 3 -r =5 => 2r =2 => r =1