Số Pythagore là số có thể viết được dạng tổng 2 số chính phương. Tìm M, N là 2 số Pythagore sao cho tổng và hiệu 2 số đó không là số Pythagore.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


10 \(\le\)n \(\le\)99 => 21 < 2n + 1 < 199 và 31 < 3n + 1 < 298
Vì 2n + 1 là số lẻ mà 2n + 1 là số chính phương
=> 2n + 1 thuộc { 25 ; 49 ; 81 ; 121 ; 169 } tương ứng số n thuộc { 12; 24; 40; 60; 84 } ( 1 )
Vì 3n + 1 là số chính phương và 31 < 3n + 1 < 298
=> 3n + 1 thuộc { 49 ; 64 ; 100 ; 121 ; 169 ; 196 ; 256 ; 289 } tương ứng n thuộc { 16 ; 21 ; 33 ; 40 ; 56 ; 65 ; 85 ; 96 } ( 2 )
Từ 1 và 2 => n = 40 thì 2n + 1 và 3n + 1 đều là số chính phương

Tham khảo:
Theo định lí cosin ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\end{array}\)
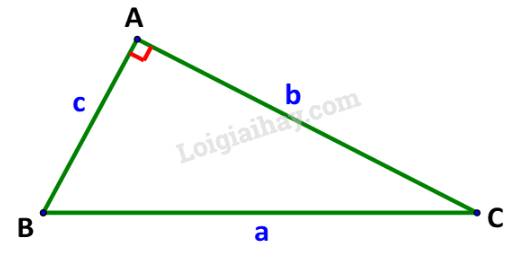
Mà \(\cos A = \cos {90^o} = 0;\cos B = \frac{c}{a};\;\cos C = \frac{b}{a}\)
\( \Rightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.0\\{b^2} = {a^2} + {c^2} - \,2a\,c.\frac{c}{a}\\{c^2} = {b^2} + {a^2} - \,2ab.\frac{b}{a}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2}\\{b^2} = {a^2} + {c^2} - \,2{a^2}\\{c^2} = {b^2} + {a^2} - \,2{b^2}\end{array} \right. \Leftrightarrow {a^2} = {b^2} + {c^2}\)
Vậy định lí Pythagore là một trường hợp đặc biệt của định lí cosin.