x^2+y^2+x-y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,=\dfrac{x^2-2xy+y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x-y}{x+y}\\ b,=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2-4y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{4xy-4y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{4y\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{4y}{x+y}\)

a) \(\left(x+y\right)^2+\left(x-y\right)^2+\left(x+y\right)\left(x-y\right)\)
\(=x^2+2xy+y^2+x^2-2xy+y^2+x^2-y^2\)
\(=3x^2+y^2\)
b)\(\left(3x+y\right)^2+\left(3x-y\right)^2-\left(2x+y\right)\left(2x-y\right)\)
\(=9x^2+6xy+y^2+9x^2-6xy+y^2-4x^2+y^2\)
\(=14x^2+3y^2\)
c) \(2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\)
\(=\left(x-y\right)^2+2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\)
\(=\left(x-y+x+y\right)^2\)
\(=4x^2\)
d)\(-2\left(x^2-9y^2\right)+\left(x-3y\right)^2+\left(x+3y\right)^2\)
\(=\left(x+3y\right)^2-2\left(x+3y\right)\left(x-3y\right)+\left(x-3y\right)^2\)
\(=\left(x+3y-x+3y\right)^2=9y^2\)

\(A=x^2-2xy+y^2+x^2+2xy+y^2+x^2-y^2=3x^2+y^2\\ B=\left(x-y-x+y-z\right)^2=\left(-z\right)^2=z^2\)

\(\left(a\right):\left(x+y\right)^2-\left(x-y\right)^2=x^2+2xy+y^2-\left(x^2-2xy+y^2\right)\\ =x^2+2xy+y^2-x^2+2xy-y^2\\ =4xy\)
\(\left(b\right):\left(x-y-z\right)^2+\left(x+y+z\right)^2\\ =\left[\left(x-y\right)-z\right]^2+\left[\left(x+y\right)+z\right]^2\\ =\left(x-y\right)^2-2z\left(x-y\right)+z^2+\left(x+y\right)^2+2z\left(x+y\right)+z^2\\ =x^2-2xy+y^2-2xz+2yz+z^2+x^2+2xy+y^2+2xz+2yz+z^2\\ =2x^2+2y^2+2z^2+4yz\)
\(\left(c\right):\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =\left(2y\right)^2=4y^2\)

\(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)
\(=\left(x+y\right)^3+3\cdot\left(x+y\right)^2\cdot\left(x-y\right)+3\cdot\left(x+y\right)\cdot\left(x-y\right)^2+\left(x-y\right)^3\)
\(=\left[\left(x+y\right)+\left(x-y\right)\right]^3\)
\(=\left(x+y+x-y\right)^3\)
\(=\left(2x\right)^3\)
\(=8x^3\)
\(---\)
\(C=8\left(x+2y\right)^3-6\left(x+2y\right)^2x+12\left(x+2y\right)x^2-8x^3\) (sửa đề)
\(=\left[2\left(x+2y\right)\right]^3-3\cdot\left(x+2y\right)^2\cdot2x+3\cdot\left(x+2y\right)\cdot\left(2x\right)^2-\left(2x\right)^3\)
\(=\left[2\left(x+2y\right)-2x\right]^3\)
\(=\left(2x+4y-2x\right)^3\)
\(=\left(4y\right)^3\)
\(=64y^3\)
\(---\)
\(D=\left(x-y\right)^3-3\cdot\dfrac{\left(x-y\right)^2}{2}\cdot y+3\cdot\dfrac{\left(x-y\right)}{4}\cdot y^2-\dfrac{y^3}{8}\)
\(=\left(x-y\right)^3-3\cdot\left(x-y\right)^2\cdot\dfrac{y}{2}+3\cdot\left(x-y\right)\cdot\left(\dfrac{y}{2}\right)^2-\left(\dfrac{y}{2}\right)^3\)
\(=\left[\left(x-y\right)-\dfrac{y}{2}\right]^3\)
\(=\left(x-y-\dfrac{y}{2}\right)^3\)
\(=\left(x-\dfrac{3}{2}y\right)^3\)
#\(Toru\)

a: =2(x-y)^3/(x-y)-7(x-y)^2/(x-y)+(x-y)/(x-y)
=2(x-y)^2-7(x-y)+1
b: =3(x-y)^5/5(x-y)^2-2(x-y)^4/5(x-y)^2+3(x-y)^2/5(x-y)^2
=3/5(x-y)^3-2/5(x-y)^2+3/5
\(a,\)
\(\left[2\left(x-y\right)^3-7\left(y-x\right)^2-\left(y-x\right)\right]:\left(x-y\right)\)
\(=\left[2\left(x-y\right)^3-7\left(x-y\right)^2+\left(x-y\right)\right]:\left(x-y\right)\)
\(=\left\{\left(x-y\right)\left[2\left(x-y\right)^2-7\left(x-y\right)+1\right]\right\}:\left(x-y\right)\)
\(=2\left(x-y\right)^2-7\left(x-y\right)+1\)
\(b,\)
\(\left[3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2\right]:\left[5\left(x-y\right)^2\right]\)
\(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)

\(a,\left(x+2\right)^2-\left(x-2\right)^2-2\left(x-2\right)\left(x+2\right).\)
\(=\left(x+2-x+2\right)^2=4^2=16\)
\(b,\left(x-y\right)^2+\left(x+y\right)^2+2\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y+x+y\right)^2=x^2\)
\(c,\left(x-y+z\right)^2-2\left(x+y\right)-2\left(x+y\right)\left(x-y\right)-z^2\)

\(A=\left(x+y\right)^2+\left(x-y\right)^2+2\left(x+y\right)\left(x-y\right)\)
\(=x^2+2xy+y^2+x^2-2xy+y^2+2\left(x^2-y^2\right)\)
\(=2x^2+2x^2=4x^2\)
Vs x = 1/2 ; y = 3 ⇒ \(A=\frac{1}{4}.4=1\)
\(B=3x^2-6xy+y^2-2x^2-4xy-2y^2-x^2+y^2=-10xy=\frac{1}{2}.3.10=15\)
\(C=x^3+3x^2y+3xy^2+y^2-x^3+3x^2y-3xy^2+y^3-6x^2y-1=2y^2-1=18-1=17\)\(D=x^3+y^3-x^3-3x^2y-3xy^2-y^3=-3x^2y-3xy^2=\frac{1}{4}.9+\frac{1}{2}.27=\frac{9}{4}+\frac{108}{4}=\frac{117}{4}\)Check lại nhé <33 sợ sai lém
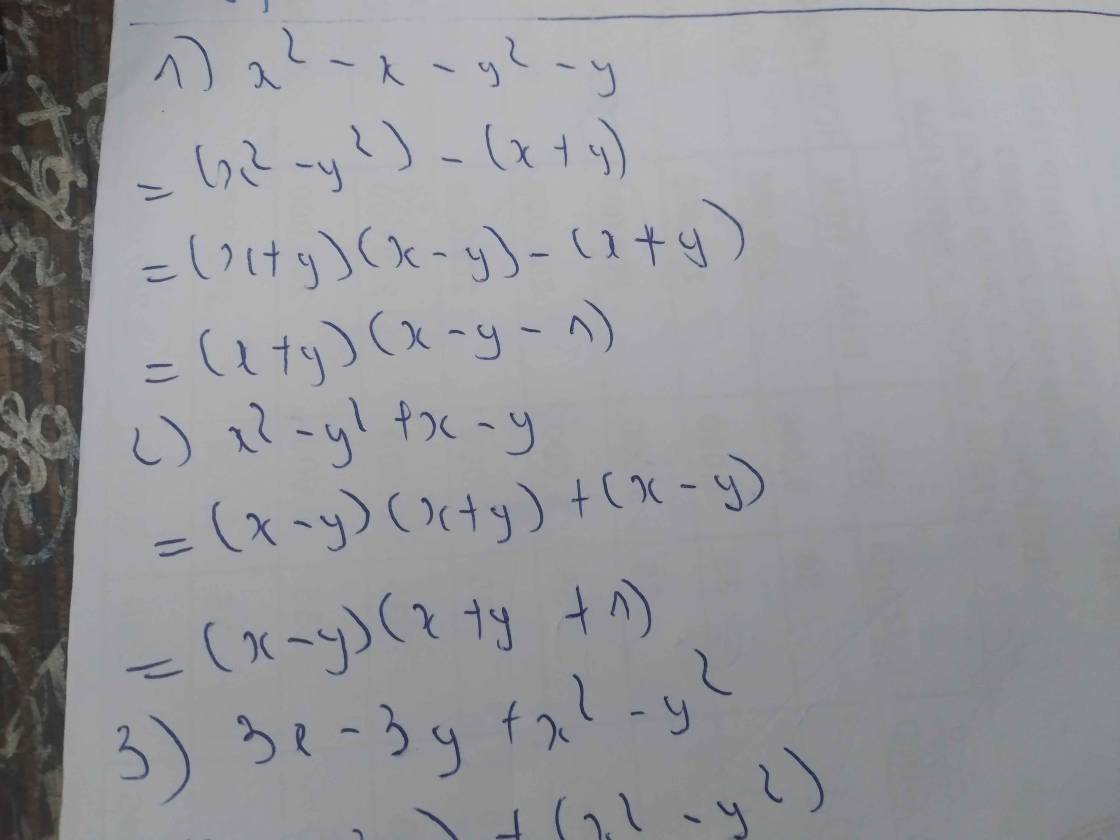
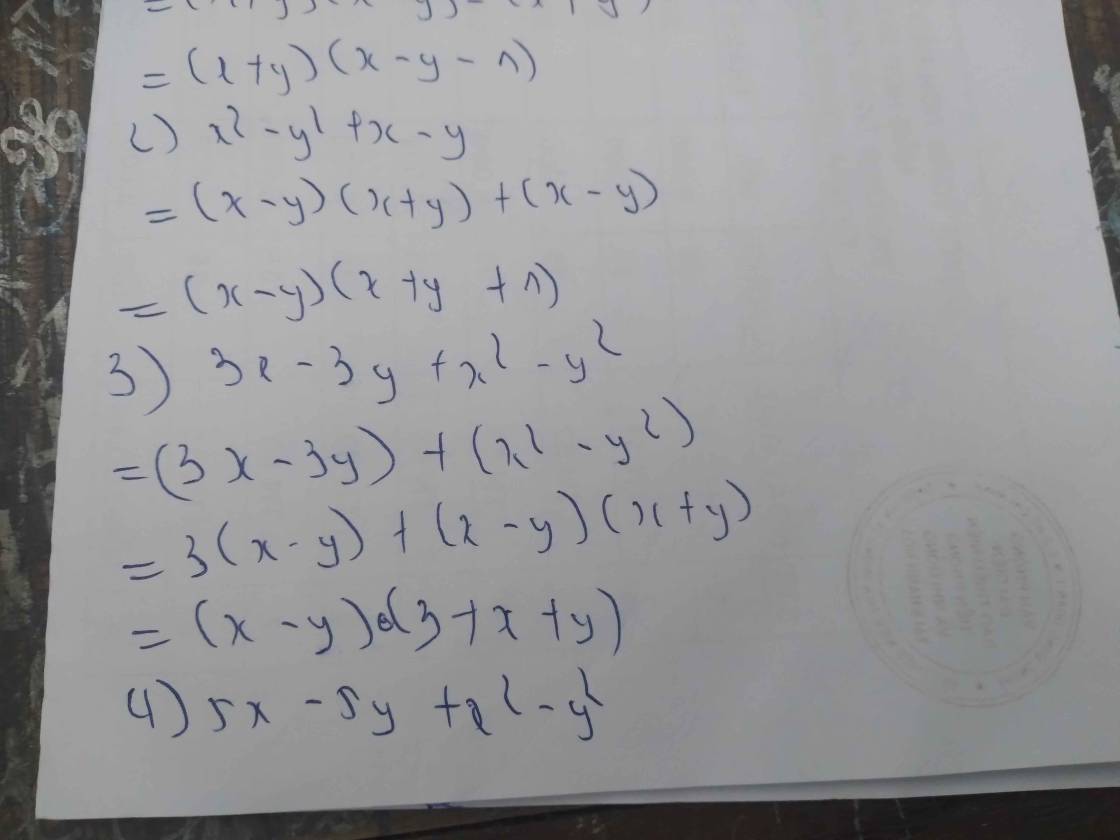
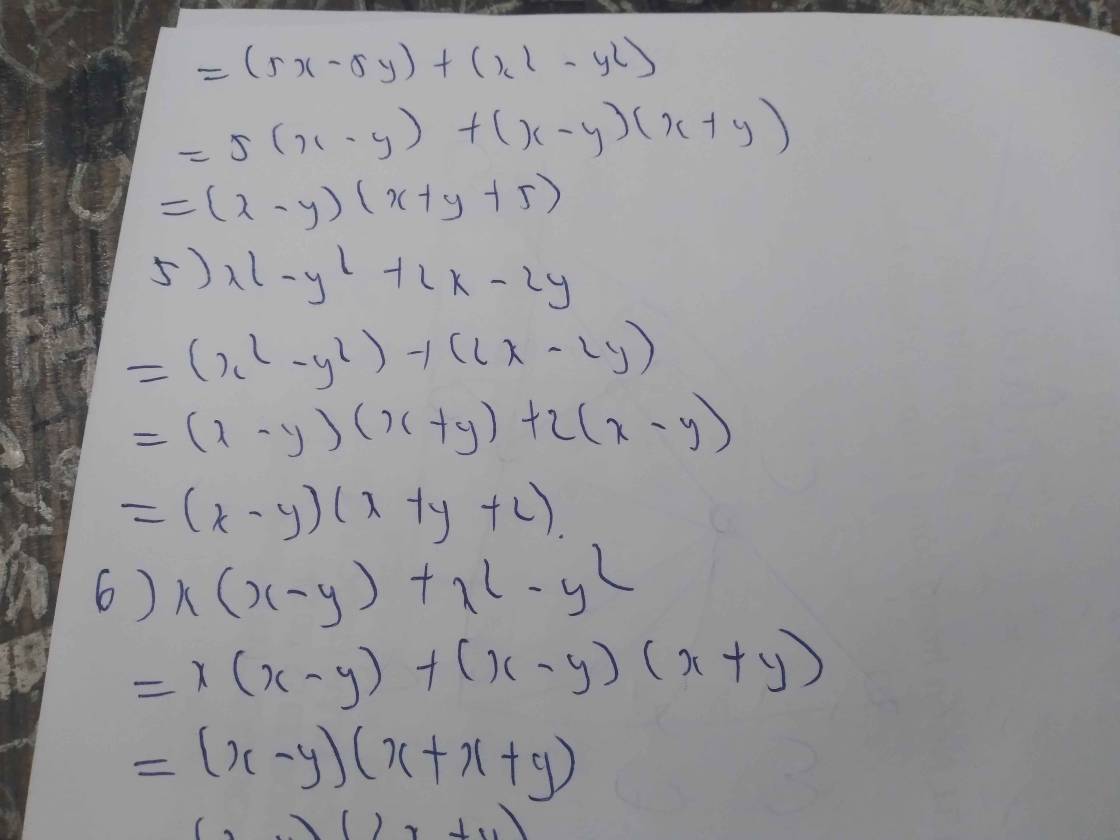
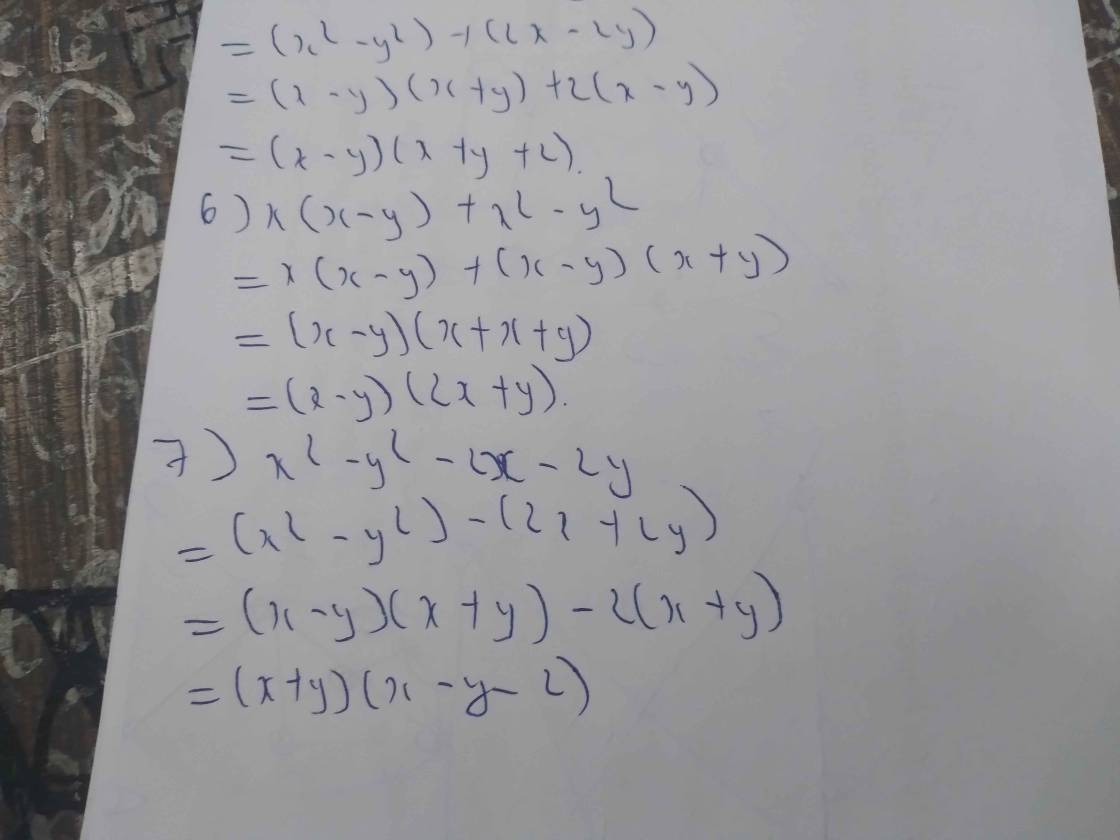
Sửa đề : \(x^2-y^2+x-y\)
\(=\left(x-y\right)\left(x+y\right)+\left(x-y\right)=\left(x-y\right)\left(x+y+1\right)\)
hay sửa như này =))
\(x^2-y^2-x-y=\left(x-y\right)\left(x+y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-1\right)\)
\(x^2-y^2+x-y\)
\(=\left(x-y\right)\left(x+y\right)+\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y+1\right)\)