y = \(\dfrac{1}{8}x^4\) - \(\dfrac{7}{4}x^2\) (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại 2 điểm phân biệt M(x1;y1), N(x2;y2) (M, N khác A) thỏa mãn:
y1 - y2 = 3(x1 - x2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Đạo hàm : y’ = 4/3.x3-28/3. x
y 2 - y 1 = 8 ( x 2 - x 1 ) ⇔ y 2 - y 1 x 2 - x 1 = 8
Vậy tiếp tuyến của (C) tại A có hệ số góc bằng 8.
+ Xét phương trình y' = 8
⇔ 4 3 x 3 - 28 3 x = 8 ⇔ 4 x 3 - 28 x - 24 = 0
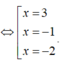
+) Với x= 3 thì A( 3; -15) nên phương trình tiếp tuyến của (C) tại A là y = 8(x-3) - 15 ( d 1 )
Phương trình hoành độ giao điểm của (C) và ( d 1 ) là
8 ( x - 3 ) - 15 = 1 3 x 4 - 14 3 x 2 ⇔ ( x - 3 ) 2 ( x 2 + 6 x + 13 ) = 0 ⇔ x = 3 .
Vậy A(3; -15) loại.
+) Với x= -2 thì A(-2; -40/3) . phương trình tiếp tuyến của (C) tại A là y = 8(x+2) - 40/3 ( d 2 )
Phương trình hoành độ giao điểm của ( C) và ( d 2 ) là
8 ( x + 2 ) - 40 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 4 x - 2 ) = 0
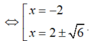
Vậy A( -2; -40/3) thỏa mãn.
+) Với x= -1 thì A( -2; -13/ 3) nên phương trình tiếp tuyến của C tại A là
y = 8(x+1) - 13/3 (d3)
Phương trình hoành độ giao điểm của C và (d3) là:
8 ( x + 1 ) - 13 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 2 x - 11 ) = 0

Vậy A( -1; -13/3) thỏa mãn.
Vậy có tất cả 2 điểm A thỏa mãn yêu cầu bài toán.
Chọn B.

Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)

Pt hoành độ giao điểm của đồ thị hàm số (C) với đường thẳng d là:
\(\dfrac{x-1}{x+1}=m-x\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\g\left(x\right)=x^2+\left(2-m\right)x-m-1=0\left(1\right)\end{matrix}\right.\)
Đồ thị (C) cắt đường thẳng d tại 2 điểm phân biệt <=> pt(1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\g\left(-1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+8>0\\-2\ne0\end{matrix}\right.\)
Khi đó: \(x_A,x_B\) là nghiệm của pt (1). Vì tiếp tuyến tại A và B //
\(\Rightarrow f'\left(x_A\right)=f'\left(x_B\right)\Leftrightarrow\dfrac{2}{\left(x_A+1\right)^2}=\dfrac{2}{\left(x_B+1\right)^2}\Leftrightarrow\left[{}\begin{matrix}x_A=x_B\left(loai\right)\\x_A+x_B=-2\end{matrix}\right.\)
Theo định lí Viet ta có:
\(x_A+x_B=m-2\Rightarrow m-2=-2\Leftrightarrow m=0\)

Gọi ![]()
phương trình tiếp tuyến của (C) tại M là
![]()
Phương trình hoành độ giao điểm:
![]()
![]()
![]()
![]()
Yêu cầu bài toán tương đương với (1) có hai nghiệm phân biệt khác
![]()
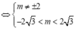
![]()
Vậy có tất cả 5 điểm có toạ độ nguyên thoả mãn.
Chọn đáp án A.

\(x^2-5x+7+2m=0\Leftrightarrow x^2-5x+7=-2m\)
Xét hàm \(f\left(x\right)=x^2-5x+7\) trên \(\left[1;5\right]\)
\(-\dfrac{b}{2a}=\dfrac{5}{2}\in\left[1;5\right]\)
\(f\left(1\right)=3\) ; \(f\left(\dfrac{5}{2}\right)=\dfrac{3}{4}\) ; \(f\left(5\right)=7\)
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb thuộc đoạn đã cho khi và chỉ khi:
\(\dfrac{3}{4}< -2m\le3\)
\(\Leftrightarrow-\dfrac{3}{2}\le m< \dfrac{3}{8}\)
Cả 4 đáp án đều sai là sao ta?

\(y'=\dfrac{-3}{\left(x-2\right)^2}\)
d. Phương trình hoành độ giao điểm
\(\dfrac{x+1}{x-2}=x-\dfrac{1}{2}\Leftrightarrow2x^2-7x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\)
Tại \(x=0\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{3}{4}\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Pttt: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)
Tại \(x=\dfrac{7}{2}\Rightarrow\left\{{}\begin{matrix}y'=-\dfrac{4}{3}\\y=3\end{matrix}\right.\) tiếp tuyến: \(y=-\dfrac{4}{3}\left(x-\dfrac{7}{2}\right)+3\)
e.
Tam giác ABC là tam giác nào nhỉ? Có lẽ đó là tam giác OAB?
g.
Giao điểm (C) với Ox có tọa độ \(\left(-1;0\right)\)
\(\Rightarrow y'\left(-1\right)=-\dfrac{1}{3}\)
Phương trình tiếp tuyến:
\(y=-\dfrac{1}{3}\left(x+1\right)\)
h.
Giao điểm (C) với Oy có tọa độ \(\left(0;-\dfrac{1}{2}\right)\)
Chính là trường hợp đầu của câu d, phương trình: \(y=-\dfrac{3}{4}x-\dfrac{1}{2}\)
\(y'=\dfrac{1}{2}x^3-\dfrac{7}{2}x\)
Chỉ cần để ý 1 lý thuyết:
Đường thẳng đi qua 2 điểm \(A\left(x_1;y_1\right)\) và \(B\left(x_2;y_2\right)\) sẽ có hệ số góc \(k=\dfrac{y_1-y_2}{x_1-x_2}\)
Do đó ta có hệ số góc của đường thẳng MN là \(k=3\)
\(\Rightarrow\dfrac{1}{2}x^3-\dfrac{7}{2}x=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-1\\x=3\end{matrix}\right.\) (sao lắm nghiệm vậy trời)
Biết hoành độ 3 tiếp điểm, bạn viết 3 pt tiếp tuyến rồi xét pt hoành độ với (C) coi cái nào có 4 nghiệm (trong đó có 1 nghiệm kép) thì nhận