với giá trị nào của a để a2+6a+22 là một số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
19 tháng 11 2017
Đáp án B
Ta có A 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos Δ φ ↔ A 1 2 + 2 A 2 cos Δ φ A 1 + A 2 2 − A 2 = 0
→ Để phương trình tồn tại nghiệm A 1 thì 2 A 2 cos Δ φ 2 − 4 A 2 2 − A 2 ≥ 0 → A 2 m a x = 12 c m
Vậy khi đó A 1 = 6 3 c m
20 tháng 2 2022
Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)
CM
24 tháng 12 2019
Ta có: x + y = a 2 + a + 1 x - y = - a 2 + a - 1 ⇔ x + y = a 2 + a + 1 2 x = 2 a ⇔ y = a 2 + 1 x = a
Do đó 3 x + y = a 2 + 3 a + 1 = a + 3 2 2 - 5 4 ≥ - 5 4 . Dấu bằng xảy ra khi a = - 3 2 .
CM
15 tháng 3 2019
Đáp án B
Đặt t = 2 sin x 2 ≥ t ≥ 0 dựa vào đường tròn lượng giác ta thấy:
Với t ∈ 0 ; 2 một giá trị của t có 6 giá trị của x
Với t = 2 một giá trị của t có 3 giá trị của x
Với t = 0 một giá trị của t có 4 giá trị của x
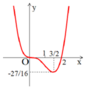
Dựa vào đồ thị ta thấy rằng PT f 2 sin x = f m có 12 nghiệm phân biệt ⇔ P T : f t = f m
có 2 nghiệm phân biệt thuộc khoảng 0 ; 2 ⇔ f m ∈ − 27 16 ; 0 ⇔ m ∈ 0 ; 2 ⇒ T = 4
12 tháng 4 2023
Δ=(a-2)^2-4(a^2-2a)
=-3a^2+4a+4
Để phương trình có hai nghiệm phân biệt thì -3a^2+4a+4<>0
=>a<>2 và a<>-2/3
|z1-z2|=|z1+z2|
=>(z1-z2)^2=(z1+z2)^2
=>z1z2=0
=>a^2-2a=0
=>a=0(nhận) hoặc a=2(loại)
=>Có 1 giá trị
13 tháng 4 2023
Giải giúp mình bài này luôn với ạ
https://hoc24.vn/cau-hoi/1-trong-mat-phang-toa-do-oxy-cho-hai-diem-a02-b42-tim-diem-m-tren-doan-thang-ab-de-parabol-p-dinh-o-va-di-qua-diem-m-chia-tam-giac-vuong-oab-thanh-hai-phan-co-dien-tich-bang-nhau2-cho-h.7896187554129
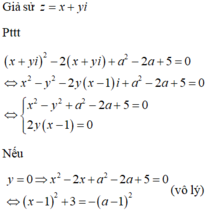
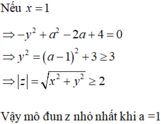
Gỉa sử tồn tại số a sao cho \(a^2+6a+22\)là một số chính phương.
\(\Rightarrow a^2+6a+22=n^2\left(n\inℕ^∗\right)\)
\(\Rightarrow\left(a^2+6a+9\right)+13=n^2\)
\(\Rightarrow\left(a+3\right)^2+13=n^2\)
\(\Rightarrow n^2-\left(a+3\right)^2=13\)
\(\Rightarrow\left(n-a-3\right)\left(n+a+3\right)=13\)
\(\Rightarrow\orbr{\begin{cases}n-a-3\\n+a+3\end{cases}}\)lẻ \(\left(1\right)\)
Mà \(n-a-3\)và \(n+a+3\)có cùng tính chẵn lẻ
\(\Rightarrow\)Mẫu thuẫn với \(\left(1\right)\)
\(\Rightarrow\)Điều giả sử là sai
\(\Rightarrow\)Không tồn tại số a sao cho \(a^2+6a+22\)là một số chính phương