Cho tam giác ABD có AB = 4, AD = 6, \(\widehat{BAD}\) = 60o. Tính độ dài của đoạn thẳng BD.
Mọi người giúp em với ạ!!! Thank you <3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

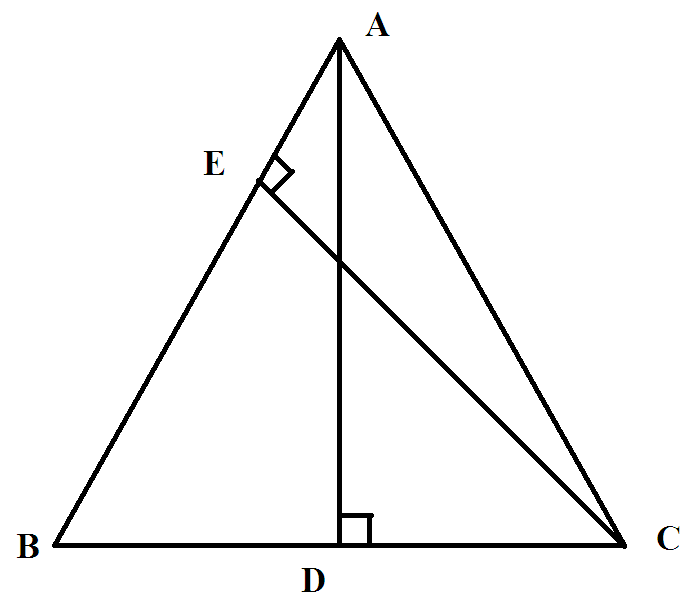
a) Xét △ABD và △CBE có:
\(\widehat{ADB}=\widehat{BEC}=90^o\)
\(\widehat{B}chung\)
Nên △ABD ∼ △CBE(g.g)
b)Theo câu a, ta có: △ABD ∼ △CB E
<=>\(\dfrac{AB}{BC}=\dfrac{BD}{BE}\Leftrightarrow AB.BE=BD.BC\)
c)Ta có:
\(BE=\dfrac{BD.BC}{AB}=\dfrac{3.12}{9}=4\left(cm\right)\)

a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)

a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)

a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
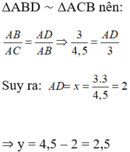
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
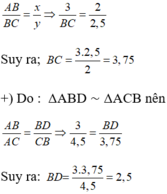
Định lý hàm cosin:
\(BD=\sqrt{AB^2+AD^2-2AB.AD.cos\widehat{BAD}}=2\sqrt{7}\)