Cho đường tròn (I;R) nội tiếp tam giác ABC. Chứng minh rằng \(abc\ge24\sqrt{3}r^3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 8 2019
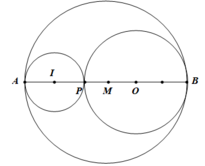
a) Điểm P, O nằm giữa A và B, AO = 4cm, BP = 4cm nên PO = 2cm, BO = 2cm.
Vậy điểm P có nằm trên đường tròn (O; 2cm).
b) Gọi M là trung điểm của AB =>AM = 3cm.
Lại có AI = 1cm => IM = 2cm
=> điểm I nằm trong đường tròn có đường kính AB ( do IM < AM ).
Có OI = 3cm > OP = 2cm nên điểm I nằm ngoài đường tròn (O; 2cm).
Vậy điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c) Đường tròn (I; 1cm) tiếp xúc với các đường tròn(O; 2cm) và đường tròn có đường kính AB
vì AP + PB = AB
CM
25 tháng 2 2017
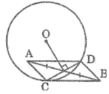
Ta có: OI ⊥ CD (gt)
Suy ra: IC = ID (đường kính dây cung)
Mà: IA = IB (gt)
Tứ giác ACBD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
TV
3 tháng 4 2016
Số học sinh lớp 6A và lớp 6B là 2/3 hay là 8/12
Khi tăng số học sinh lớp 6A thêm 8 bạn, lớp 6B lên 4 bạn thì tỉ số là 3/4 hay là 9/12
vậy lớp 6 A thêm số học sinh hơn lớp 6B là 8 - 4 = 4 bạn
4 bạn ứng với số phần là: 9/12 - 8/12 = 1/12
Lớp 6A có số học sinh là: 4x 12 - 8 = 40 (hs)
Lớp 6B có số học sinh là: 40x 3 : 2= 60 (hs)
