Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Đặt:n_{Al}=a\left(mol\right),n_{Fe}=b\left(mol\right)\)
\(m_{hh}=27a+56b=8.3\left(g\right)\left(1\right)\)
\(n_{H_2}=\dfrac{5.6}{22.4}=0.25\left(mol\right)\)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
\(Tathấy:\)
\(n_{HCl}=2n_{H_2}=2\cdot0.25=0.5\left(mol\right)\)
\(V_{ddHCl}=\dfrac{0.5}{0.2}=2.5\left(l\right)\)
\(n_{H_2}=1.5a+b=0.25\left(mol\right)\left(2\right)\)
\(\left(1\right),\left(2\right):a=b=0.1\)
\(C_{M_{AlCl_3}}=\dfrac{0.1}{2.5}=0.04\left(M\right)\)
\(C_{M_{FeCl_2}}=\dfrac{0.1}{2.5}=0.04\left(M\right)\)
Chúc em học tốt !!!
a, Ta có: \(n_{H_2}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
BTNT H, có: \(n_{HCl}=2n_{H_2}=0,5\left(mol\right)\)
\(\Rightarrow V_{HCl}=\dfrac{0,5}{0,2}=2,5\left(l\right)\)
b, Giả sử: \(\left\{{}\begin{matrix}n_{Al}=x\left(mol\right)\\n_{Fe}=y\left(mol\right)\end{matrix}\right.\)
⇒ 27x + 56y = 8,3 (1)
Các quá trình:
\(Al^0\rightarrow Al^{+3}+3e\)
x___________ 3x (mol)
\(Fe^0\rightarrow Fe^{+2}+2e\)
y____________2y (mol)
\(2H^++2e\rightarrow H_2^0\)
______0,5__0,25 (mol)
Theo ĐLBT mol e, có: 3x + 2y = 0,5 (2)
Từ (1) và (2) ⇒ x = y = 0,1 (mol)
BTNT Al và Fe, có: \(\left\{{}\begin{matrix}n_{AlCl_3}=n_{Al}=0,1\left(mol\right)\\n_{FeCl_3}=n_{Fe}=0,1\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow C_{M_{AlCl_3}}=C_{M_{FeCl_3}}=\dfrac{0,1}{2,5}=0,04M\)
Bạn tham khảo nhé!

Gọi nFe = a (mol); nAl = b (mol)
=> 56a + 27b = 11 (1)
nH2 = 8,96/22,4 = 0,4 (mol)
PTHH:
Fe + 2HCl -> FeCl2 + H2
a ---> 2a ---> a ---> a
2Al + 6HCl -> 2AlCl3 + 3H2
b ---> 1,5b ---> b ---> b
=> a + 1,5b = 0,4 (2)
Từ (1)(2) => a = 0,1 (mol); b = 0,15 (mol)
mFe = 0,1 . 56 = 5,6 (g)
mAl = 0,2 . 27 = 5,4 (g)
THAM KHẢO :
Fe + 2HCl -> FeCl2 + H2 (1)
a) 2Al + 6HCl -> 2AlCl3 + 3H2 (2)
Gọi khối lượng Fe là x(g) (0<x<11) => nFe = x/56 (mol)
Thì mAl là 11-x(g) => nAl = (11-x)/27 (mol)
nH2 = 8,96/22,4 = 0,4 (mol)
Theo PT (1) ta có: nH2 = nFe = x/56 (mol)
Theo PT (2) ta có: nH2 = 3/2 nAl = 3/2 . (11-x)/27 = (11-x)/18 (mol)
Theo đề bài, nH2 thu được là 0,4(mol) nên ta có:
x/56 + (11-x)/18 = 0,4
<=> 18x +56(11-x) = 403,2
<=> x = 5,6 (g)
Do đó: mFe = 5,6(g) => nFe = 5,6/56 = 0,1 (mol)
mAl = 11-5,6 = 5,4(g) => nAl = 5,4/27 = 0,2 (mol)

\(2Al+6HCl->2AlCl_3+3H_2\\ Fe+2HCl->FeCl_2+H_2\\ n_{Al}=a;n_{Fe}=b\\ 27a+56b=8,3\\ 1,5a+b=\dfrac{5,6}{22,4}=0,25\\ a=b=0,1\\ m_{Al}=27\cdot0,1=2,7g\\ m_{Fe}=8,3-2,7=5,6g\\ a=\dfrac{3a+2b}{500}\cdot36,5=3,65\%\\ m_{ddsau}=508,3-0,25\cdot2=507,8g\\ C\%_{AlCl_3}=\dfrac{133,5a}{507,8}=2,63\%\\ C\%_{FeCl_2}=\dfrac{127b}{507,8}=2,50\%\)




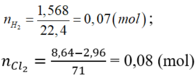
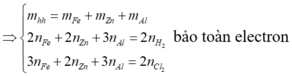
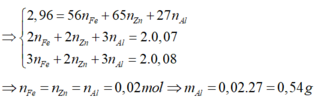
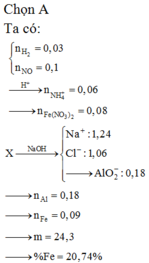
Gọi a,b lần lượt là số mol của Al, Fe trong hỗn hợp ban đầu
=> 27a+56b=8,3 (1)
\(n_{H_2}=\dfrac{5,6}{22,4}=0,25mol\)
Ta có quá trình trao đổi elcetron
\(Al^0\rightarrow Al^{+3}+3e\)
a----------------3a--(mol)
\(Fe^0\rightarrow Fe^{+2}+2e\)
b----------------2b--(mol)
\(2H^{-1}+2e\rightarrow H_2^0\)
----------0,5------0,25-(mol)
Áp dụng định luật bảo toàn e ta có: 3a+2b=0,5 (2)
Giải hệ phương trình gồm (1) và (2) ta được: \(\left\{{}\begin{matrix}a=0,1\\b=0,1\end{matrix}\right.\)
\(\left[{}\begin{matrix}m_{Al}=0,1\cdot27=2,7g\\m_{Fe}=0,1\cdot56=5,6g\end{matrix}\right.\)