Chứng minh A=2+22+23+...+229+230 chia hết cho 3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KJ
1
15 tháng 12 2021
\(2A=2-2^2+2^3-...-2^{30}+2^{31}\\ \Leftrightarrow2A+A=2-2^2+2^3-...-2^{30}+2^{31}+1-2+2^2-...-2^{29}+2^{30}\\ \Leftrightarrow3A=2^{31}+1\\ \Leftrightarrow A=\dfrac{2^{31}+1}{2}\)
CM
7 tháng 7 2019
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
10 tháng 10 2021
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
S
0
13 tháng 11 2023
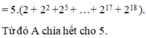
1: \(A=2+2^2+2^3+2^4+...+2^{97}+2^{98}+2^{99}+2^{100}\)
\(=2\left(1+2+2^2+2^3\right)+...+2^{97}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{97}\right)\)
\(=30\left(1+2^4+...+2^{96}\right)⋮30\)
2:
\(B=3+3^2+3^3+...+3^{2022}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2021}+3^{2022}\right)\)
\(=\left(3+3^2\right)+3^2\left(3+3^2\right)+...+3^{2020}\left(3+3^2\right)\)
\(=12\left(1+3^2+...+3^{2020}\right)⋮12\)
E
19 tháng 3 2021
Ta có :
\(A=2+2^2+2^3+2^4...2^{2010}\)\(^0\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(=2.3+2^3.3+....+2^{2009}.3\)
\(=3\left(2+2^3+....+2^{2009}\right)⋮3\)
Ta có :
\(2+2^2+2^3+2^4+....+2^{2010}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(=2.7+2^4.7+....+2^{2008}.7\)
\(=7\left(2+2^4+....+2^{2008}\right)⋮7\)
Vậy \(2^1+2^2+2^3+2^4+...+2^{2010}⋮3\) và \(7\)
NN
2
21 tháng 11 2021
A=\((1+2)+\left(2^2+2^3\right)+...+\left(2^{19}+2^{20}\right)\)
A=\(3.1+2^2\left(1+2\right)+...+2^{19}\left(1+2\right)\)
A=\(3.1+3.2^2+...+3.2^{19}\)
A=\(3\left(1+2^2+...+2^{19}\right)\)\(⋮3\)
Vậy A\(⋮3\)
21 tháng 11 2021
A=(1+2)+(22+23)+...+(219+220)(1+2)+(22+23)+...+(219+220)
A=3.1+22(1+2)+...+219(1+2)3.1+22(1+2)+...+219(1+2)
A=3.1+3.22+...+3.2193.1+3.22+...+3.219
A=3(1+22+...+219)3(1+22+...+219)⋮3⋮3
NÊN A⋮3
TN
1
AH
Akai Haruma
Giáo viên
13 tháng 12 2021
Lời giải:
$A=(2+2^2)+(2^3+2^4)+....+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+...+2^{99}(1+2)$
$=2.3+2^3.3+...+2^{99}.3$
$=3(2+2^3+...+2^{99})\vdots 3$
Ta có đpcm.
10 tháng 10 2021
\(B=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+...+2^{58}\right)⋮7\)
OY
21 tháng 8 2021
b) A=2+22+23+...+220
A=(2+22)+(23+24)+...+(219+220)
A=3.2+3.23+...+3.219
A=3.(2+23+25+...+219)
⇒A⋮3
phần c) làm tương tự
NG
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 10 2023
a) \(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(A=2\cdot\left(1+3\right)+2^3\cdot\left(1+3\right)+...+2^{59}\cdot\left(1+3\right)\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy A chia hết cho 3
________
\(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\)
Vậy A chia hết cho 5