Tifm hệ số lớn nhất trong khia triển thành đa thức của (1/3+3/4x)4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2023
Hệ số lớn nhất sẽ tương ứng với số hạng đứng chính giữa
=>Hệ số lớn nhất là \(C^{51}_{101}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
\(f\left(x\right)=\sum\limits^3_{i=0}C_3^i\left(x+x^2\right)^i.\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k\left(2x\right)^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}C_3^i.C_i^jx^j.\left(x^2\right)^{i-j}\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k.2^k.x^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}\sum\limits^{15}_{k=0}C_3^iC_i^jC_{15}^k\left(\dfrac{1}{4}\right)^{3-i}.2^k.x^{2i+k-j}\)
Số hạng chứa \(x^{13}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le i\le3\\0\le j\le i\\0\le k\le15\\2i+k-j=13\end{matrix}\right.\)
\(\Rightarrow\left(i;j;k\right)=\left(0;0;13\right);\left(1;0;12\right);\left(1;1;11\right);\left(2;0;11\right);\left(2;1;10\right);\left(2;2;9\right);\left(3;0;10\right);\left(3;1;9\right)\)
\(\left(3;2;8\right);\left(3;3;7\right)\) (quá nhiều)
Hệ số....
CT
Cô Tuyết Ngọc
Manager
VIP
10 tháng 1 2023
Em muốn hỏi bài nào vậy? Quá nhiều bài thầy cô và các bạn không thể trả lời được hết em ạ
1 tháng 8 2023
a: P=2+25x^2-3x^3+4x^2-2x-x^3+6x^5
=6x^5-4x^3+29x^2-2x+2
b: bậc của P(x) là 5
c: hệ số lớn nhất là 6
Hệ số tự do là 2
P(-1)=-6+4+29+2+2=29+2=31
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2021
\(C_2^2+C_3^2+...+C_n^2=C_3^3+C_3^2+C_4^2+...+C_n^2\) (do \(C_2^2=C_3^3=1\))
\(=C_4^3+C_4^2+C_5^2+...+C_n^2=C_5^3+C_5^2+...+C_n^2\)
\(=...=C_n^3+C_n^2=C_{n+1}^3\)
Do đó:
\(2C_{n+1}^3=3A_{n+1}^2\Leftrightarrow\dfrac{2.\left(n+1\right)!}{3!.\left(n-2\right)!}=\dfrac{3.\left(n+1\right)!}{\left(n-1\right)!}\)
\(\Leftrightarrow n-1=9\Rightarrow n=10\)
\(\Rightarrow P=\left(1-x-3x^3\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(-x-3x^3\right)^k\)
\(=\sum\limits^{10}_{k=0}C_{10}^k\left(-1\right)^k\left(x+3x^3\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^kx^i.3^{k-i}.x^{3\left(k-i\right)}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^k.3^{k-i}.x^{3k-2i}\)
Ta có: \(\left\{{}\begin{matrix}0\le i\le k\le10\\i;k\in N\\3k-2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;2\right);\left(4;4\right)\)
Hệ số: \(C_{10}^2C_2^1\left(-1\right)^2.3^1+C_{10}^4C_4^4.\left(-1\right)^4.3^0=...\)
HT
11 tháng 4 2021
\(\Rightarrow he-so:\left[{}\begin{matrix}C^9_{10}C^1_9\left(-3\right)^{10-9}\left(-1\right)=270\\C^{10}_{10}C^4_{10}\left(-3\right)^{10-10}.\left(-1\right)^4=210\end{matrix}\right.\)
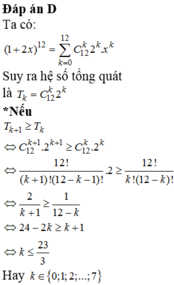
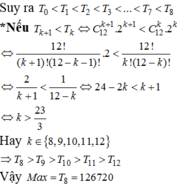
\(\left(\dfrac{1}{3}+\dfrac{3}{4}x\right)^4=\sum\limits^4_{k=0}C^k_4.\left(\dfrac{1}{3}\right)^{4-k}.\left(\dfrac{3}{4}\right)^k.x^k\)
Nhị thức Newton có 1 đặc điểm là hệ số khi tăng đến số cao nhất sẽ ko tăng nữa mà giảm dần, từ đó ta giả sử \(a_n\) là hệ số lớn nhất\(\Rightarrow\left\{{}\begin{matrix}a_n\ge a_{n+1}\\a_n\ge a_{n-1}\end{matrix}\right.\)
\(a_n=C^{n-1}_4.\left(\dfrac{1}{3}\right)^{5-n}.\left(\dfrac{3}{4}\right)^{n-1}\)
\(a_{n-1}=C^{n-2}_4.\left(\dfrac{1}{3}\right)^{6-n}.\left(\dfrac{3}{4}\right)^{n-2}\)
\(a_{n+1}=C^n_4.\left(\dfrac{1}{3}\right)^{4-n}.\left(\dfrac{3}{4}\right)^n\)
\(\Rightarrow\left\{{}\begin{matrix}C^{n-1}_4.\left(\dfrac{1}{3}\right)^{5-n}.\left(\dfrac{3}{4}\right)^{n-1}\ge C^{n-2}_4.\left(\dfrac{1}{3}\right)^{6-n}.\left(\dfrac{3}{4}\right)^{n-2}\\C^{n-1}_4.\left(\dfrac{1}{3}\right)^{5-n}.\left(\dfrac{3}{4}\right)^{n-1}\ge C^n_4.\left(\dfrac{1}{3}\right)^{4-n}.\left(\dfrac{3}{4}\right)^n\end{matrix}\right.\)
Bạn tự khai triển nốt nhé, sẽ chặn được k là xong. Mà thú thiệt, mấy bài kiểu này cứ mode-7 rồi nhập hàn là xong :)