vẽ các điểm trên mặt phẳng tọa độ
A(1,5;3) M(0;2) P(-1,5;-1,5)
B(-2;4) C(-2;5) N(4;0)
giúp mình vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QH
1
12 tháng 12 2023
a:
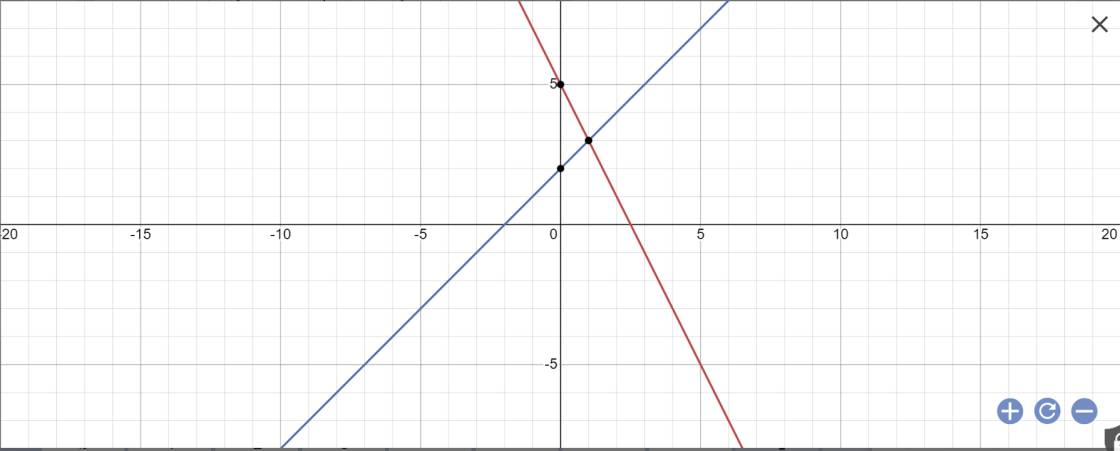
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6
25 tháng 3 2021
a) Ta có: \(\widehat{BOC}+\widehat{AOB}+\widehat{AOC}=360^0\)
\(\Leftrightarrow\widehat{BOC}+150^0+150^0=360^0\)
hay \(\widehat{BOC}=60^0\)
Vậy: \(\widehat{BOC}=60^0\)
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
Áp dụng định lý Pitago: $OA=\sqrt{1^2+1^2}=\sqrt{2}$
Vì $B\in Ox$ nên tọa độ của $B$ có dạng $(b,0)$
Vì $B$ thuộc đường tròn tâm $O$ bán kính $OA=\sqrt{2}$ nên $|x_B|=OB=OA=\sqrt{2}$. Vậy $B(\pm \sqrt{2},0)$
$C\in Oy$ nên $C$ có tọa độ $(0,c)$
$C$ thuộc đường tròn đường kính $OA$ nên:
$|y_C|=OC=OA=\sqrt{2}$. Vậy $C(0, \pm \sqrt{2})$
AH
Akai Haruma
Giáo viên
18 tháng 12 2021
Lời giải:
a.
Đồ thị xanh lá: $y=2x+1$
Đồ thị xanh dương: $y=x-3$
b.
PT hoành độ giao điểm:
$y=2x+1=x-3$
$\Leftrightarrow x=-4$
$y=x-3=(-4)-3=-7$
Vậy tọa độ điểm $M$ là $(-4;-7)$