Xác định giá trị của tham số m để hàm số
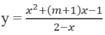
nghịch biến trên mỗi khoảng xác định của nó
A. m = −1; B. m > 1;
C. m ∈ (−1;1); D. m ≤ −5/2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D.
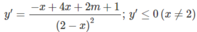
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.

Đáp án B
TXĐ: D = ℝ \ m − 2 . Ta có:
y ' = m 2 − m + 8 x − m + 2 2 > 0 ⇔ − m 2 + 2 m + 8 > 0
⇔ − 2 < m < 4 → m ∈ ℤ m = − 1 ; 0 ; 1 ; 2 ; 3 .
Do đó có 5 giá trị nguyên của m.

Đáp án A
Ta có: y ' = 3 x 2 - 6 m x ⇒ y ' = 0 ⇔ x = 0 h o ặ c x = 2 m
TH1: m < 0
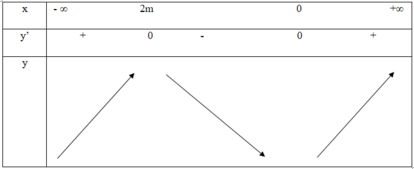
Dễ thấy hàm số trên đoạn (0;1) đồng biến với mọi m < 0
TH2: m = 0
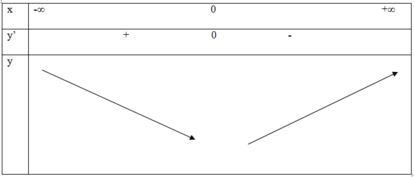
Dễ thấy hàm số trên đoạn (0;1) đồng biến với mọi m = 0
TH3: m > 0
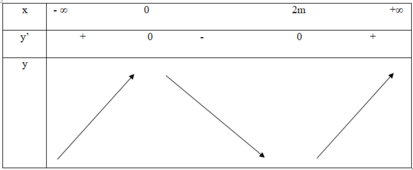
Dễ thấy hàm số trên đoạn (0;1) nghịch biến ⇔ 2 m ≥ 1

Đáp án D.
P T f x = m vô nghiệm ⇔ − 2 ≤ m ≤ 1 ⇔ m ∈ − 2 ; 1 .

Đáp án A.
Ta có f x − m = 0 ⇔ f x = m . Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f x và đường thẳng y = m .Do đó để phương trình đã cho có nghiệm duy nhất thì đường thẳng y = m phải cắt đồ thị hàm số y = f x tại một điểm duy nhất. Khi đó m ∈ 3 ; + ∞ .
Đáp án: D.
⇔ Δ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.