Tính phần thực phần ảo của số phức x, biết:
z = 1 - πi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


| Số phức Phần thực Phần ảo | ||
| -3 + 5i | -3 | 5 |
| 4 - i 2 | 4 | - 2 |
| 0 + πi | 0 | π |
| 1 + 0i | 1 | 0 |

Mỗi số phức là một biểu thức z = a + bi với a, b ∈ R, i 2 = -1
- Số thực a là phần thực của số phức: z = a + bi
- Số thực b là phần ảo của số phức z = a + bi
- Môđun của số phức z = a + bi là 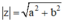

a) Phần thực z1 – 2z2 là – 3, phần ảo của nó là 8.
b) Phần thực và phần ảo của z1.z2 tương ứng là 26 và 7.

- Mỗi biểu thức dạng a+bi, trong đó a, b ∈ R, i2= -1 được gọi làm một số phức.
- Với số phức z = a + bi, ta gọi a là phần thực, số b gọi là phần ảo của z.
- Ta có z = a + bi thì môdun của z là |z|=|a+bi|=√a2+b2
Phần thực: 1, phần ảo: -π