PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 4 2017
Tập hợp các điểm biểu diễn các số phức z là các hình sau:
a) Ta có x = 1, y tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng x = 1 (hình a)
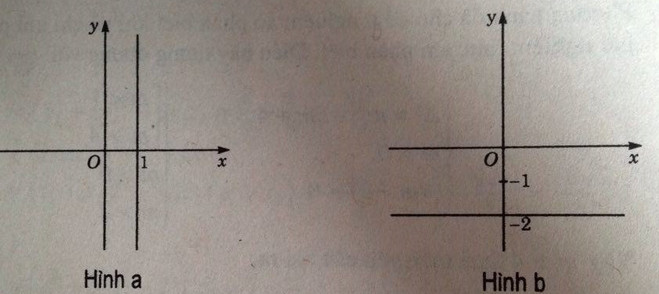
b) Ta có y = -2, x tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng y = -2 (hình b)
c) Ta có x ∈ [-1, 2] và y ∈ [0, 1] nên tập hợp các điểm biểu diễn z là hình chữ nhật sọc (hình c)
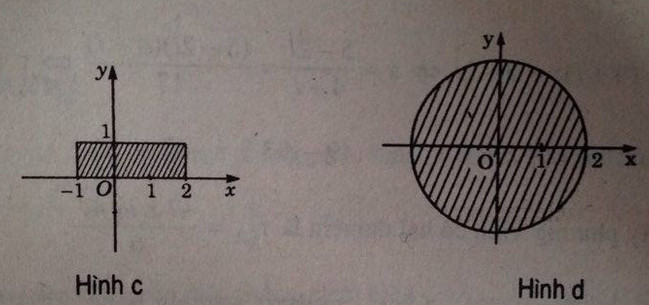
d) Ta có:
|z|≤2⇔√x2+y2≤2⇔x2+y2≤4|z|≤2⇔x2+y2≤2⇔x2+y2≤4
Vậy tập hợp các điểm biểu diễn z là hình tròn tâm O (gốc tọa độ) bán kính bằng 2 (kể cả các điểm trên đường tròn) (hình d)
PV
0
7 tháng 7 2018
ta có : \(\overline{Z}=\left(\sqrt{2}+i\right)^2\left(1-\sqrt{2}i\right)\)
\(\Leftrightarrow\overline{Z}=\left(1+2\sqrt{2}i\right)\left(1-\sqrt{2}i\right)=5-\left(\sqrt{2}-2\sqrt{2}\right)i\)
\(\Rightarrow Z=5+\left(\sqrt{2}-2\sqrt{2}\right)i\)
\(\Rightarrow\) phần ảo của số phức \(Z\) là \(\sqrt{2}-2\sqrt{2}\)
1 tháng 4 2017
Giả sử z = a + bi
Khi đó: |z|=√a2+b2|z|=a2+b2
Từ đó suy ra:
|z|=√a2=|a|≥a,|z|=√b2=|b|≥b
PT
1
Phần thực: 2 2 , phần ảo: 0