Cho đường tròn (O), dây BC không đi qua O, A thuộc cung lớn BC, M là điểm chính giữa cung nhỏ BC, tiếp tuyến tại M và C của đường tròn cắt nhau tại N. AB cắt CM tại K, AM cắt CN tại P.
CM tứ giác ACPK nội tiếp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 4 2019
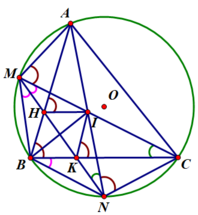
1) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.
Ta có M là điểm chính giữa cung A B ⏜ ⇒ A M ⏜ = B M ⏜ ⇒ M N A ^ = M C B ^
⇒ K N I ^ = I C K ^ . Tứ giác CNKJ có C và N là 2 đỉnh kề nhau cùng nhìn cạnh KJ dưới góc bằng nhau nên CNKJ nội tiếp (dấu hiệu nhận biết tứ giác nội tiếp)
Do đó bốn điểm C, N, K, I cùng thuộc một đường tròn.
CM
23 tháng 8 2018
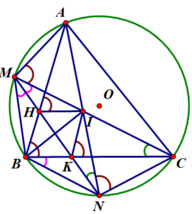
3) Chứng minh tứ giác BHIK là hình thoi.
Ta có A B C ^ = A N C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
Mà A M C ^ = A H I ^ (góc nội tiếp cùng chắn cung I C ⏜ )
⇒ A B C ^ = I K C ^ Mà 2 góc này ở vị trí đồng vị nên H B / / I K (1)
+ Chứng minh tương tự phần 1 ta có tứ giác AMHI nội tiếp
A N C ^ = I K C ^ (góc nội tiếp cùng chắn cung A I ⏜ )
Ta có A B C ^ = A M C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
⇒ A B C ^ = A H I ^ Mà 2 góc này ở vị trí đồng vị nên B K / / H I (2)
Từ (1) và (2) suy ra tứ giác BHIK là hình bình hành.
Mặt khác AN, CM lần lượt là các tia phân giác của các góc A và C trong tam giác ABC nên I là giao điêm 3 đường phân giác, do đó BI là tia phân giác góc B
Vậy tứ giác BHIK là hình thoi (dấu hiệu nhận biết hình thoi).
CM
8 tháng 9 2018
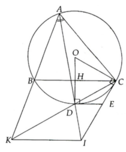
a, AD là phân giác B A C ^
=> D là điểm chính giữa B C ⏜ => OD ⊥ BC
Mà DE là tiếp tuyến => ĐPCM
b, E C D ^ = 1 2 s đ C D ⏜ = D A C ^ = B A D ^ => Đpcm
c, HC = P 3 2 => H O C ^ = 60 0 => B O C ^ = 120 0
=> l B C ⏜ = π . R . 120 0 180 0 = 2 3 πR
CM
13 tháng 5 2018
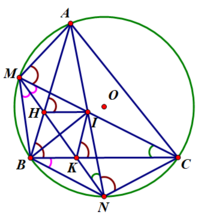
2) Chứng minh N B 2 = N K . N M .
Ta có N là điểm chính giữa cung B C ⏜ ⇒ B N ⏜ = C N ⏜ ⇒ B M N ^ = C M N ^ (góc nội tiếp chắn 2 cung bằng nhau)
Mà C B N ^ = C M N ^ (góc nội tiếp chắn cùng chắn cung C N ⏜ )
C B N ^ = B M N ^ (cùng bằng góc C M N ^ ) ⇒ K B N ^ = B M N ^
Xét Δ K B N v à Δ B M N có:
N ^ chung
K B N ^ = B M N ^
⇒ Δ K B N ∽ Δ B M N ⇒ K N B N = B N M N ⇒ N B 2 = N K . N M
(điều phải chứng minh).
Xét đường tròn (O), ta có M là điểm chính giữa của cung nhỏ BC \(\Rightarrow\widebat{MB}=\widebat{MC}\)
Xét tiếp đường tròn (O) có \(\widehat{BAM}\)và \(\widehat{CAM}\)là các góc nội tiếp lần lượt chắn các cung MB và MC của (O). Mà \(\widebat{MB}=\widebat{MC}\left(cmt\right)\)\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)(trong 1 đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Lại xét đường tròn (O) có CP là tiếp tuyến tại C và dây cung CM \(\Rightarrow\widehat{PCM}=\frac{1}{2}sđ\widebat{CM}\)(góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn).
Mặt khác \(\widehat{CAM}\)là góc nội tiếp chắn \(\widebat{CM}\)nên \(\widehat{CAM}=\frac{1}{2}sđ\widebat{CM}\)(trong 1 đường tròn, góc nội tiếp chắn một cung bằng nửa số đo cung bị chắn)
\(\Rightarrow\widehat{PCM}=\widehat{CAM}\left(=\frac{1}{2}sđ\widebat{CM}\right)\)
Mà \(\widehat{CAM}=\widehat{BAM}\left(cmt\right)\Rightarrow\widehat{PCM}=\widehat{BAM}\left(=\widehat{CAM}\right)\Rightarrow\widehat{PCK}=\widehat{KAP}\)
Xét tứ giác ACPK có \(\widehat{PCK}=\widehat{KAP}\left(cmt\right)\)
\(\Rightarrow\)Tứ giác ACPK nội tiếp (tứ giác có hai đỉnh kề nhìn cạnh đối diện dưới dạng các góc bằng nhau thì tứ giác đó nội tiếp)
Bạn ơi, mình vừa mới nghĩ ra cách làm này bạn xem giúp mình có đúng ko ạ,
Xét đường tròn (O) có:
∠APC và ∠AKC là 2 góc có đỉnh nằm ngoài đường tròn,
=> \(\text{∠}APC=\frac{sd\widebat{AC}-sd\widebat{MC}}{2}\)
\(\text{∠}AKC=\frac{sd\widebat{AC}-sd\widebat{MB}}{2}\)
Mà M là điểm nằm giữa cung nhỏ BC
\(=>\widebat{MC}=\widebat{MB}\)
Vậy suy ra ∠APC = ∠AKC
=> Tứ giác ACPK nội tiếp