Giải phương trình 2x4 – 17x2 – 9 = 0
GHi rõ bước ra nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
1
20 tháng 7 2021
\(2x^4-7x^3+17x^2-20x+14\)
\(=2x^4-3x^3+7x^2-4x^3+6x^2-14x+4x^2-6x+14\)
\(=x^2\left(2x^2-3x+7\right)-2x\left(2x^2-3x+7\right)+2\left(2x^2-3x+7\right)\)
\(=\left(x^2-2x+2\right)\left(2x^2-3x+7\right)\)
CM
7 tháng 7 2019
Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm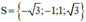 
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
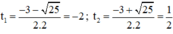
t 1 = - 2 < 0 nên loại.
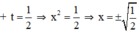
Vậy phương trình có tập nghiệm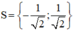 
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
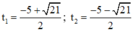
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
GQ
3
10 tháng 11 2021
\(\left[{}\begin{matrix}x+5=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=3\end{matrix}\right.\)
10 tháng 11 2021
\(a,\Rightarrow\left(x-3\right)\left(x+5\right)=0\Rightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\\ b,\Rightarrow x^2-x-2x+2=0\\ \Rightarrow\left(x-2\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
TN
18 tháng 6 2017
Đk: tự tìm
\(pt\Leftrightarrow\sqrt{\left(x-4\right)\left(x+4\right)}+\sqrt{x-4}=0\)
\(\Leftrightarrow\sqrt{x-4}\left(\sqrt{x+4}+1\right)=0\)
Dễ thấy: \(\sqrt{x+4}\ge0\forall x\)
\(\Rightarrow\sqrt{x+4}+1\ge1>0\forall x\) (vô nghiệm)
\(\Rightarrow\sqrt{x-4}=0\Rightarrow x-4=0\Rightarrow x=4\)
TV
giải phương trình bất nhất (3x-1)(x+3)= (2-x)(5-3x) các bạn ghi các bước giải ra giúp mik luôn nha !
5
SS
19 tháng 1 2022
(3x-1)(x+3)= (2-x)(5-3x)
\(\Leftrightarrow3x^2+9x-x-3=10-6x-5x+3x^2\)
\(\Leftrightarrow3x^2+8x-3-10+11x-3x^2=0\)
\(\Leftrightarrow19x-13=0\)
\(\Leftrightarrow x=\frac{13}{19}\)
Vậy \(x\in\left\{\frac{13}{19}\right\}\)
PT
1
CM
13 tháng 4 2019
2x4 – 3x2 – 2 = 0; (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 2t2 – 3t – 2 = 0 (2)
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = (-3)2 - 4.2.(-2) = 25 > 0
⇒ Phương trình có hai nghiệm
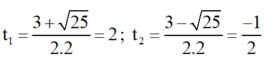
Chỉ có giá trị t1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
3 tháng 1 2022
\(\Leftrightarrow\left\{{}\begin{matrix}-x+3y=1\\2\left(x-3y\right)=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3y=-1\\x-3y=-1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)
dat a=x2
suy ra p/t tuong duong
2a2-17a-9=0
giai phuong trinh ta duoc hai nghiem: 9 ;-1/2
vi dat nhu tren nen a khong nhan gia tri am nen -1/2 (loai)
a=9 nhan
suy ra x2=9
suy ra x=-3 hoac x=3
nhan ca hai nghiem
À hèn chi mình thấy còn -1/2 sao ko tính thì ra là vậy :)) Cám ơn