Cho số phức z = a + b i (a,b là các số thực) thỏa mãn z . z + 2 z + i = 0. Tính giá trị của biểu thức T = a + b 2 .
A. T = 4 3 − 2
B. T = 3 + 2 2
C. T = 3 − 2 2
D. T = 4 + 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Phương pháp giải: Lấy môđun hai vế để tìm z ,thế ngược lại để tìm số phức z
Lời giải:
Ta có ![]()
Lấy môđun 2 vế, ta được ![]()
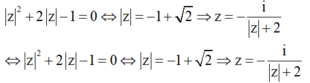
z = - i - 1 + 2 + 2 = - i 1 + 2 = ( 1 - 2 ) i ⇒ a = 0 b = 1 - 2
Vậy ![]()

Đáp án C
a 2 + b 2 ( a + b i ) + 2 ( a + b i ) + i = 0 ⇔ a a 2 + b 2 + 2 a + ( b a 2 + b 2 + 2 b + 1 ) i = 0 ⇔ a a 2 + b 2 + 2 a = 0 b a 2 + b 2 + 2 b + 1 = 0 ⇒ a = 0 b = 1 ± 2 ⇒ a = 0 b = 1 − 2 ⇒ T = 1 - 2 2 = 3 − 2 2

Đáp án D
Phương pháp giải:
Đặt z=a+bi thực hiện yêu cầu bài toán, chú ý số phức là số thực khi phần ảo bằng 0
Lời giải:
Ta có ![]()
Khi đó
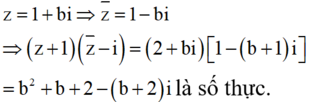
Khi và chỉ khi b + 2 = 0 ⇔ b = - 2
Vậy S=a+2b= -3
Đáp án C