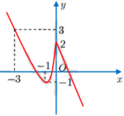
Cho hàm số y = f(x) liên tục trên ℝ có đồ thị như hình vẽ bên. Xét hàm số g x = f x + 3 x − 1 + 2 m . Tìm m để giá trị lớn nhất của g(x) trên đoạn [-1;0] bằng 1.
A. m = - 1
B. m = - 2
C. m = - 1 2
D. m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
![]()
![]()
![]()
Từ đồ thị hàm số ta có ![]()
Theo yêu cầu bài toán ta cần có: ![]()
Chọn A.

\(g’\left( x \right) = \left( {3{x^2} + 1} \right)f’\left( {{x^3} + x – 1} \right)\)
Xét \(g’\left( x \right) = 0 \Leftrightarrow f’\left( {{x^3} + x – 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^3} + x – 1 = – 1\\{x^3} + x – 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} + x = 0\\{x^3} + x – 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).
\(\begin{array}{l}g\left( 0 \right) = f\left( { – 1} \right) + m = 3 + m\\g\left( 1 \right) = f\left( 1 \right) + m = – 1 + m\end{array}\)
\(\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right)\\ \Rightarrow 3 + m = – 10\\ \Leftrightarrow m = – 13\end{array}\)

Chọn A
Ta có: g(x) = f(x-2017) - 2018x + 2019.
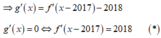
Nhận xét: tịnh tiến đồ thị hàm số y = f'(x) sang bên phải theo phương của trục hoành 2017 đơn vị ta được đồ thị hàm số y = f'(x-2017) . Do đó, số nghiệm của phương trình f'(x) = 2018 bằng số nghiệm của phương trình (*).
Dựa vào đồ thị ta thấy phương trình (*) có nghiệm đơn duy nhất hay hàm số đã cho có duy nhất 1 điểm cực trị.

Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.

Đặt g ( x ) = 3 f ( x ) - x 3 . Hàm số ban đầu có dạng y=|g(x)|
Ta có g ' ( x ) = 3 f ' ( x ) - 3 x 2 .
Cho g'(x)=0 ⇔ [ x = 0 x = 1 x = 2

Dễ thấy g(0)=0. Ta có bảng biến thiên
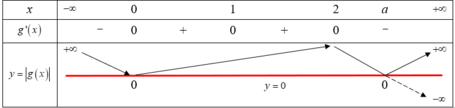
Dựa vào BBT suy ra hàm số y=|g(x)| đồng biến trên khoảng (0;2) và a ; + ∞ với g(a)=0
Chọn đáp án C.
Đáp án là A