Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có
S d = 9 π S x q = 15 π ⇔ π r 2 = 9 π π r l = 15 π ⇔ r = 3 l = 5 ⇒ h = 4 ⇒ V = 1 3 π r 2 h = 12 π
Đáp án B
Diện tích xung quang của hình trụ là: S 1 = 2 π R . R 3 = 2 π R 2 3
Độ dài đường sinh của hình nón là: l = R 2 + R 3 2 = 2 R
Diện tích xung quanh của hình nón là: S 2 = π R l = π R .2 R = 2 π R 2
Tính tỉ số giữa diện tích xung quang của hình trụ và diện tích xung quanh của hình nón
S 1 S 2 = 2 π R 2 3 2 π R 2 = 3
Đáp án A
Giả sử thiết diện là một tam giác cân có độ dài chiều cao hạ từ đỉnh nón xuống đáy tam giác là x ( 0 < x < R 2 + h 2 )
Khi đó ta dễ dàng tính được độ dài đáy tam giác theo x, h và R là:
2 R 2 + h 2 - x 2
Do đó, diện tích S của tam giác là:
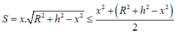(BĐT Cauchy)
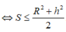
Vậy S m a x = R 2 + h 2 2
Đáp án D
Theo bài ra, ta có 4 3 π R 3 = 1 3 π R 2 h ⇔ 4 R = h ⇔ h R = 4
Đáp án B
Theo giả thiết, ta có r = 1 ⇒ l = 2 r 2 = 2 ⇒ S x q = π r l = 2 π