Cho hàm số y = 2 x + 1 x - 2 C . Tập hợp tất cả các giá trị của tham số m để đường thẳng y = x + m cắt đồ thị (C) tại hai điểm thuộc hai nhánh là:.
A. - ∞ ; - 1 2
B. - 1 2 ; ∞
C. ℝ \ - 1 2
C. R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương trình hoành độ giao điểm: m x + 1 = x - 3 x + 1 ⇔ x ≢ 1 m x + 1 x + 1 = x - 3
⇔ x ≢ - 1 m x 2 + m x + 4 = 0 ( * )
Để đường thẳng y = m x + 1 cắt đồ thị hàm số y = x - 3 x + 1 tạo hai điểm phân biệt thì phương trình (*) phải có hai nghiệm phân biệt khác -1
⇔ m ( - 1 ) 2 + m . ( - 1 ) + 4 ≢ 0 ∆ = m 2 - 16 m > 0 ⇔ m ( m - 16 ) > 0 ⇔ m > 16 m < 0

Chọn D.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
![]()
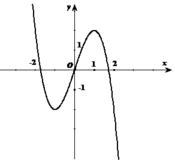
Ta khảo sát hàm số (C): y = -x3 + 3x có đồ thị sau như hình bên.
Tìm được ![]() nên yêu cầu bài toán
nên yêu cầu bài toán
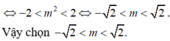
Đường thẳng y = x + m cắt đồ thị (C) tại hai điểm thuộc hai nhánh
Phương trình y = 2 x + 1 x - 2 C có 2 nghiệm phân biệt x 1 ; x 2 thỏa mãn: x 1 < 2 < x 2
Vậy, đường thẳng y = x + m cắt đồ thị (C) tại hai điểm thuộc hai nhánh với mọi m ∈ R .
Chọn: D