Cho hàm số y = 2 x 2 − 3 x + m x − m có đồ thị (C) . Tìm tất cả các giá trị của m để (C) không có tiệm cận đứng.
A. m=0 hoặc m=1
B.m=2
C.m=0
D.m=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
.
.
CM
4 tháng 7 2018
Chọn D
Đồ thị hàm số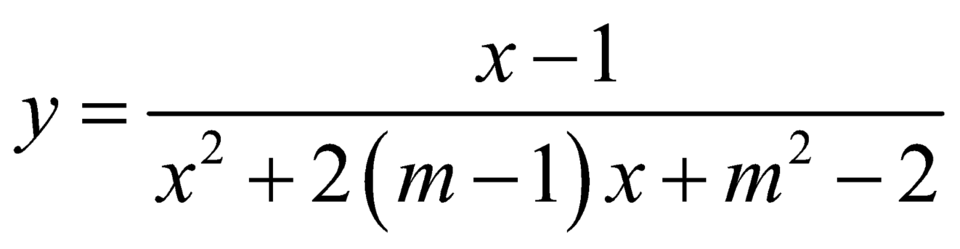 
có đúng hai tiệm cận đứng
có 2 nghiệm phân biệt khác 1.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
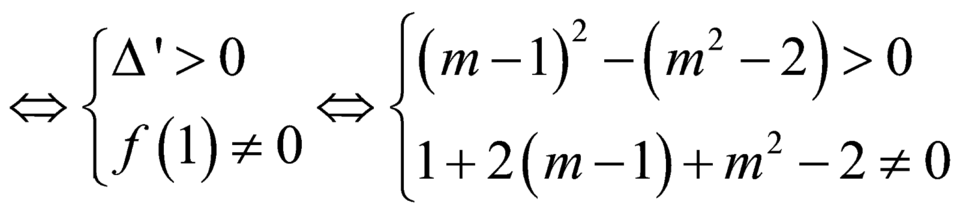
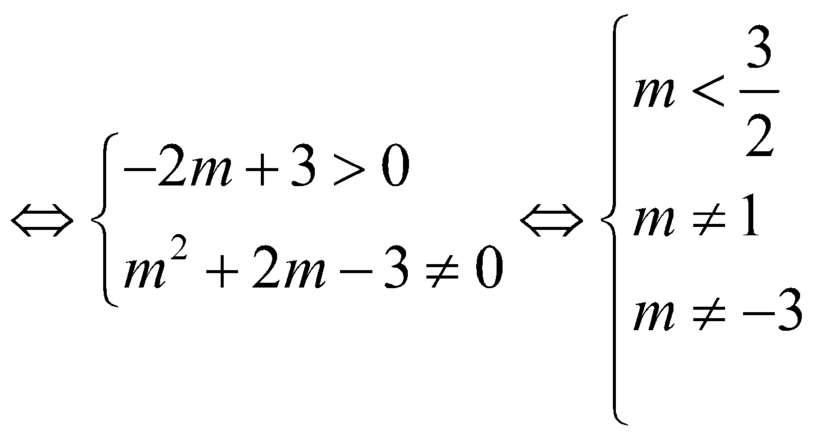
Do mẫu có bậc 2 còn tử bậc 1 \(\Rightarrow\)hàm không có tiệm cận đứng khi và chỉ khi phương trình \(x^2-2mx+1=0\) vô nghiệm
\(\Leftrightarrow\Delta'=m^2-1< 0\)
\(\Rightarrow-1< m< 1\)
CM
17 tháng 11 2019
Đáp án B(Cm) có hai đường tiệm cận đứng 
có hai nghiệm phân biệt khác 1
Đáp án A
Hàm số không có tiệm cận đứng ⇔ 2 x 2 − 3 x + m = 0 có nghiệm
⇔ 2 m 2 − 3 m + m = 0 ⇔ m m − 1 = 0 ⇒ m = 0 m = 1