Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , S A = a 3 vuông góc với (ABCD). Tính góc giữa hai đường thẳng SB và CD.
A. 60 0
B. 30 0
C. 45 0
D. 90 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
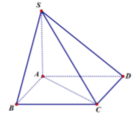
Ta có ABCD là hình bình hành => AB//CD
Do đó (SB,CD) = (SB,AB) = SBA
Vì SA ⊥ (ABCD) => SA ⊥ AB => ∆ SAB vuông tại A.
Xét tam giác vuông SAB ta có: ![]()
Vậy (SB;CD) = 60 °

Chọn đáp án A
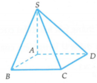
Ta có ABCD là hình bình hành nên CD//AB.
Lại có S A ⊥ A B C D ⇒ S A ⊥ A B
⇒ ∆ S A B vuông tại A.
Suy ra
![]()
Trong tam giác SAB vuông tại A có
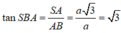
⇒ S B A ⏜ = 60 0

Đáp án B
Hướng dẫn giải:
+)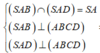
![]()
![]()
+) ![]()
![]()
+) Ta có A B ⊥ B C , kẻ A P ⊥ S B ( P ∈ S B )
d(A;(SBC)) = AP ⇒ d(AD;SB) = AP
+) 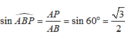
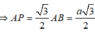
![]()

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)

Chọn đáp án A

Từ kẻ đường thẳng vuông góc với SC cắt SC tại K.
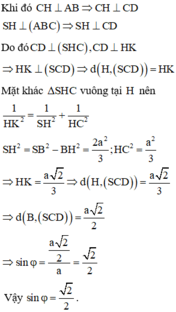


Đáp án: D.
Hướng dẫn giải:
Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định
![]()
S A ⊥ B C ⊥ A M
![]()
⇒ A H ⊥ S M ⇒ A H ⊥ ( S B C )
⇒ d ( A , ( S B C ) ) = A H
Vì AD//(SBC) chứa BC nên
d(SB,AD)=d(AD,(ABC))=d(A,(SBC))=AH
Tính: SA=AD= a 2 ,AM= a 2
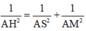
⇒ A H = a 2 5
Đáp án là A