Cho tứ diện ABCD,M,N lần lượt là trung điểm của AB và BC, P là điểm trên cạnh CD sao cho CP=2PD Mặt phẳng (MNP) cắt AD tại Q. Tính tỷ số A Q Q D .
A. 1 2
B. 3
C. 2 3
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 11 2017
Đáp án A
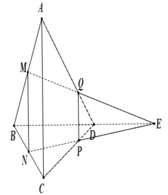
Gọi 
thì Q là giao điểm của (MNP) và AD.
Áp dụng định lí Menelaus trong ∆ B C D ta có:
Áp dụng định lí Menelaus trong ∆ ABD ta có:
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 12 2020
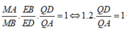
Trong mp (ABD) nối PM kéo dài cắt BD tại I
Áp dụng định lý Menelaus cho tam giác ABD:
\(\dfrac{PA}{PD}.\dfrac{DI}{IB}.\dfrac{BM}{MA}=1\Leftrightarrow\dfrac{1}{3}.\dfrac{ID}{IB}.1=1\)
\(\Leftrightarrow\dfrac{ID}{IB}=3\)
CM
1 tháng 8 2018
Đáp án D
Ta chia khối đa diện thành các khối tứ diện
Thể tích khối tứ diện đều đã cho là V o = 2 12
HT
25 tháng 12 2020
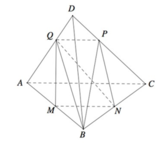
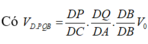
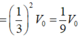
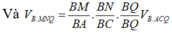
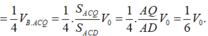
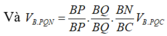
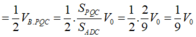
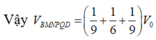
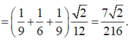
Ta sẽ áp dụng Menelaus cho 2 tam giác BCD và ABC
À quên cái dạo đầu :v
Vì lười chụp hình nên đánh máy vậy
Tìm giao điểm giữa CD và (MNQ) trước
Gán CD vô (BCD) => giao tuyến giữa (BDC) và (MNQ) là QK (K là giao điểm của MN với BC)
=> QK cắt CD tại P => (MNQ) cắt CD tại P
Rồi giờ áp dụng Menelaus cho tam giác ABC trước
\(\dfrac{AM}{MB}.\dfrac{BK}{KC}.\dfrac{CN}{NA}=1\Leftrightarrow\dfrac{1}{2}.\dfrac{BK}{KC}.1=1\Rightarrow BK=2KC\)
Áp dụng Menelaus cho tam giác BCD
\(\dfrac{BK}{KC}.\dfrac{CP}{PD}.\dfrac{DQ}{QB}=1\Leftrightarrow2.\dfrac{CP}{PD}.1=1\Rightarrow CP=\dfrac{1}{2}PD\)
\(\Rightarrow\dfrac{CP}{CD}=\dfrac{1}{3}\)
Đáp án A