Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
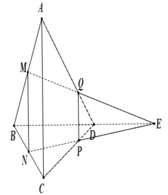
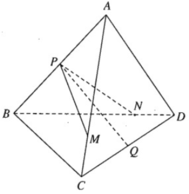
Gọi ![]() thì Q là giao điểm của (MNP) và AD.
thì Q là giao điểm của (MNP) và AD.
Áp dụng định lí Menelaus trong ∆ B C D ta có:
![]()
![]()
Áp dụng định lí Menelaus trong ∆ ABD ta có:
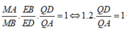
![]()

Trong mp (ABD) nối PM kéo dài cắt BD tại I
Áp dụng định lý Menelaus cho tam giác ABD:
\(\dfrac{PA}{PD}.\dfrac{DI}{IB}.\dfrac{BM}{MA}=1\Leftrightarrow\dfrac{1}{3}.\dfrac{ID}{IB}.1=1\)
\(\Leftrightarrow\dfrac{ID}{IB}=3\)

Đáp án C
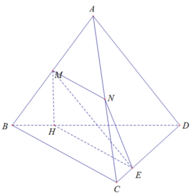
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang

Đáp án A
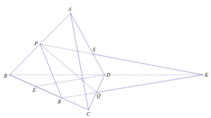
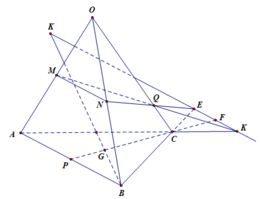
Xét (BCD) có: RQ ∩ BD = K
⇒ K ∈ (ABD)
Xét (ABD) có: PK ∩ AD = S
Gọi E là trung điểm BR
⇒ R là trung điểm đoạn EC
Mà Q là trung điểm CD
⇒ RQ là đường trung bình tam giác DEC
⇒ RQ // DE ⇒ RK // DE
Xét tam giác BRK có: RK // DE và E là trung điểm BR
⇒ D là trung điểm BK
Xét tam giác ABK có: AD là đường trung tuyến cạnh BK
và KP là đường trung tuyến cạnh AB
PK ∩ AD = S
⇒ S là trọng tâm tam giác ABK
⇒ S A S D = 2

A B C D M N E O K
Ta có
\(E\in MN\) mà \(MN\in\left(OMN\right)\Rightarrow E\in\left(OMN\right)\)
\(O\in\left(OMN\right)\)
\(\Rightarrow EO\in\left(OMN\right)\)
Ta có
\(E\in BD\) mà \(BD\in\left(BCD\right)\Rightarrow E\in\left(BCD\right)\)
\(O\in\left(BCD\right)\)
\(EO\in\left(BCD\right)\)
Trong (BCD) kéo dài EO cắt CD tại K
=> \(K\in\left(OMN\right);K\in CD\) => K chính là giao của CD với (OMN)

Đáp án D
![]()
Ta chia khối đa diện thành các khối tứ diện
![]()
Thể tích khối tứ diện đều đã cho là V o = 2 12
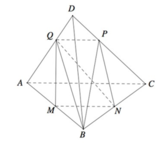
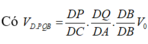
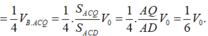
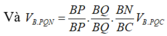
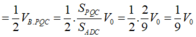
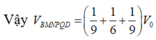

Ta có:
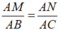
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)


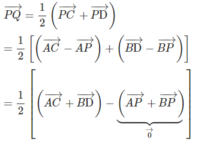
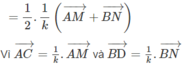
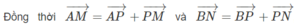
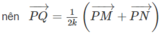
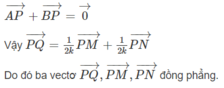
Ta sẽ áp dụng Menelaus cho 2 tam giác BCD và ABC
À quên cái dạo đầu :v
Vì lười chụp hình nên đánh máy vậy
Tìm giao điểm giữa CD và (MNQ) trước
Gán CD vô (BCD) => giao tuyến giữa (BDC) và (MNQ) là QK (K là giao điểm của MN với BC)
=> QK cắt CD tại P => (MNQ) cắt CD tại P
Rồi giờ áp dụng Menelaus cho tam giác ABC trước
\(\dfrac{AM}{MB}.\dfrac{BK}{KC}.\dfrac{CN}{NA}=1\Leftrightarrow\dfrac{1}{2}.\dfrac{BK}{KC}.1=1\Rightarrow BK=2KC\)
Áp dụng Menelaus cho tam giác BCD
\(\dfrac{BK}{KC}.\dfrac{CP}{PD}.\dfrac{DQ}{QB}=1\Leftrightarrow2.\dfrac{CP}{PD}.1=1\Rightarrow CP=\dfrac{1}{2}PD\)
\(\Rightarrow\dfrac{CP}{CD}=\dfrac{1}{3}\)