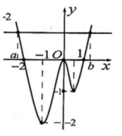
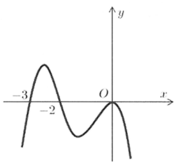
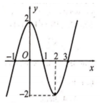
Cho hàm số y=f(x) xác định và liên tục trên R. Đồ thị của hàm số y=f'(x) hình trên. Kết luận nào sau đây về tính đơn điệu của hàm số y = f x − 2 x + 2018 là đúng?

A. Hàm số đồng biến trên R
B. Hàm số đồng biến trên các khoảng − ∞ ; 0
C. Hàm số đồng biến trên khoảng 1 ; + ∞
D. Hàm số nghịch biến trên khoảng − 1 ; 5

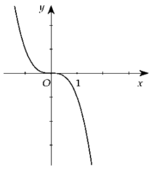
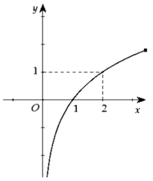


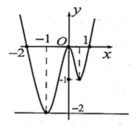
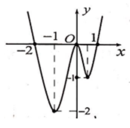



Đáp án C
Ta có y ' = f ' x − 2 dựa trên đồ thị ta thấy x ∈ 1 ; + ∞ ⇒ f ' x > 2 ⇒ f ' x − 2 > 0 ⇒ y đồng biến