Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , A D = 2 a . Đường cao SA bằng 2a. Khoảng cách từ trung điểm M của SB đến mặt phẳng (SCD) bằng
A. d = a 2 2
B. d = a 2
C. d = 3 a 2 2
D. d = 3 a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H=h/c(S,(ABCD)) ta có ∆ S H A = ∆ S H B ( c - g - c ) ⇒ H A = H B vì vậy H nằm trên đường trung trực của đoạn thẳng AB đồng thời cũng là đường trung trực của CD.

Gọi M,N lần lượt là trung điểm các cạnh AB,CD. Hạ ![]()
Tam giác SMN có MN=2a, ![]() và đường cao hạ từ đỉnh M là
và đường cao hạ từ đỉnh M là
MK=d(M,(SCD))=d(A,(SCD))=a. Do đó
M
K
=
S
M
=
a
⇒
K
≡
S
. Vì vậy
∆
S
M
N
vuông tại ![]() a.
a.
Vì vậy 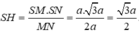
Do đó ![]()
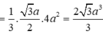
Chọn đáp án A.

Chọn đáp án C
HC là hình chiếu của SC lên mặt phẳng (ABCD).
Góc giữa SC với mặt phẳng (ABCD) là: S C H ^ = 45 °
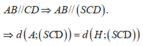
Kẻ 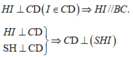
Kẻ 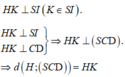
Ta có: ![]()
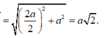
Tam giác SHC vuông cân tại H vì ![]()
Mặt khác: HI = AD = a
Xét tam giác SHI vuông tại H: 
![]()
![]()

Chọn B.
Phương pháp:
Gắn hệ trục tọa độ.
Cách giải:
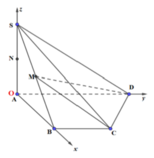

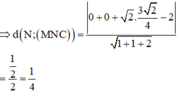
Vây, khoảng cách từ N đến mặt phẳng (MCD) bằng: 1 4 a
Đáp án A
Kẻ A H ⊥ S D H ∈ S D ⇒ A H ⊥ S C D ⇒ d A ; S C D = A H = a 2 .
Mà M là trung điểm của S B ⇒ d M ; S C D = 1 2 d A ; S C D = a 2 2 .