Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi G 1 là giao điểm của AG và mp(BCD), G 2 là giao điểm của BG và mp(ACD). Khẳng định nào sau đây là đúng?
A. G 1 G 2 / / A B
B. G 1 G 2 / / A C
C. G 1 G 2 / / C D
D. G 1 G 2 / / A D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

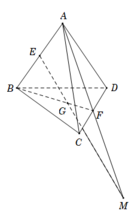
Vì G là trọng tâm tam giác BCD và F là trung điểm của CD nên G thuộc (ABF)
Ta có E là trung điểm của AB nên E thuộc ( ABF).
Gọi M là giao điểm của EG và AF mà A F ⊂ A C D suy ra M thuộc (ACD).
Vậy giao điểm của EG và mp (ACD) là giao điểm M của EG và AF
Chọn B.

Đáp án C.
+ Gọi G 0 là trọng tâm tam giác BCD=> G B ⇀ + G C ⇀ + G D ⇀ = 3 G G 0 ⇀
=>
G
A
⇀
+
G
B
⇀
+
G
C
⇀
+
G
D
⇀
=
0
⇀
![]()
=> A, G, G 0 thẳng hàng ⇒ G 0 = G A
+ Có A, G,
G
A
thẳng hàng mà ![]()

Đáp án C
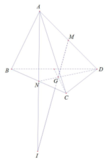
Xét (AND) có MG ∩ AN = I
Mà AN ∈ (ABC)
⇒ MG ∩ (ABC) = I
Đáp án A.
Hình vẽ dễ thấy tính song song là: G 1 G 2 ∥ A B
Chứng minh
Vì G G 1 G A = G G 2 G B = 1 4 ⇒ G 1 G 2 ∥ A B