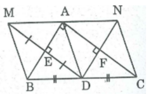
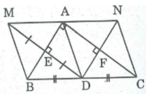
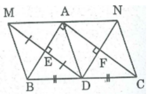
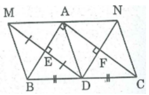
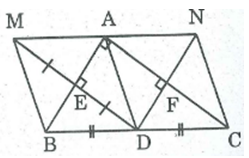
Cho tam giác ABC vuông tại A , điểm D là trung điểm của BC . Gọi M là điểm đối xứng với D qua AB , E là giao điểm của DM và AB . Gọi N là điểm đối xứng với D qua AC , F là giao điểm của DN và AC
a) Tứ giác AEDF là hình gì ? Vì sao ?
b) Các tứ giác ADBM , ADCN là hình gì ? Vì sao ?
c) Chứng minh : M đối xứng với N qua A
d) Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông