Biết rằng đường thẳng y = 2x + 2m luôn cắt đồ thị hàm số y = x 2 + 3 x + 1 tại hai điểm phân biệt A, B với mọi giá trị của tham số m. Tìm hoành độ trung điểm của AB?
A. m + 1
B. -m - 1
C. -2m - 2
D. -2m + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án DPhương trình hoành độ gaio điểm của đồ thị (C) và đường thẳng 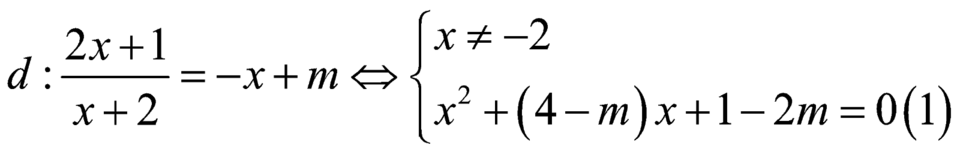
Gọi ![]() . Ta tính được
. Ta tính được ![]() khi m = 0
khi m = 0

Lời giải:
PT hoành độ giao điểm:
$\frac{-4x+12}{x+1}=2x+m$
$\Rightarrow -4x+12=(2x+m)(x+1)$
$\Leftrightarrow 2x^2+x(m+6)+m-12=0(*)$
Ta thấy:
\(2(-1)^2+(-1)(m+6)+m-12=-16\neq 0\)
$\Delta (*)=(m+6)^2-8(m-12)=m^2+4m+132=(m+2)^2+128>0$ với mọi $m$
$\Rightarrow (*)$ luôn có 2 nghiệm pb khác -1 với mọi $m$
Tức là $(d)$ cắt $(C)$ tại 2 điểm phân biệt với mọi $m$ (đpcm)

a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
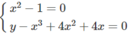
Giải hệ, ta được hai nghiệm:
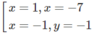
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
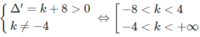

Đáp án là B.
Phương trình hoàng độ giao điểm của
C & d : x + m 2 x − 1 = − x + 1 ; x ≠ 1 2
⇔ 2 x 2 + 2 m x − m − 1 = 0 (1)
C & d cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt và khác 1 2 .
Khi đó: m 2 + 2 m + 2 > 0 − 1 2 ≠ 0 ⇔ m ∈ ℝ .
Đáp án là B