Gọi S là tập hợp giá trị thực của tham số m sao cho phương trình z 2 - m + 4 z + m 2 + 3 = 0 có nghiệm phức z 0 thỏa mãn z 0 = 2 . Số phần tử của tập hợp S là
A. 4
B. 3
C. 2
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


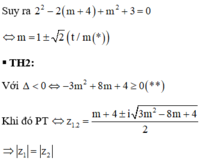


\(z^2-2\left(2m-1\right)z+m^2=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}z_1+z_2=-\dfrac{b}{a}=2\left(2m-1\right)=4m-2\\z_1z_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
Ta có :
\(z^2_1+z_2^2=2\)
\(\Leftrightarrow\left(z_1+z_2\right)^2-2z_1z_2=2\)
\(\Leftrightarrow\left(4m-2\right)^2-2m^2-2=0\)
\(\Leftrightarrow16m^2-16m+4-2m^2-2=0\)
\(\Leftrightarrow14m^2-16m+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=\dfrac{1}{7}\end{matrix}\right.\)
Ta có phương trình bậc hai trên tập số phức:
z^2 - 2(2m-1)z + m^2 = 0
Theo định lý giá trị trung bình, nếu z1 và z2 là nghiệm của phương trình trên, thì ta có:
z1 + z2 = 2(2m-1) và z1z2 = m^2
Từ phương trình z1^2 + z2^2 = 2, ta suy ra:
(z1+z2)^2 - 2z1z2 = 4
Thay z1+z2 và z1z2 bằng các giá trị đã biết vào, ta được:
(2(2m-1))^2 - 2m^2 = 4
Đơn giản hóa biểu thức ta có:
m^2 - 4m + 1 = 0
Suy ra:
m = 2 + √3 hoặc m = 2 - √3
Vậy, để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, ta cần phải có m = 2 + √3 hoặc m = 2 - √3.
Kết luận: Có hai giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, đó là m = 2 + √3 hoặc m = 2 - √3.

Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
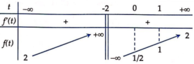
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng