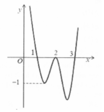
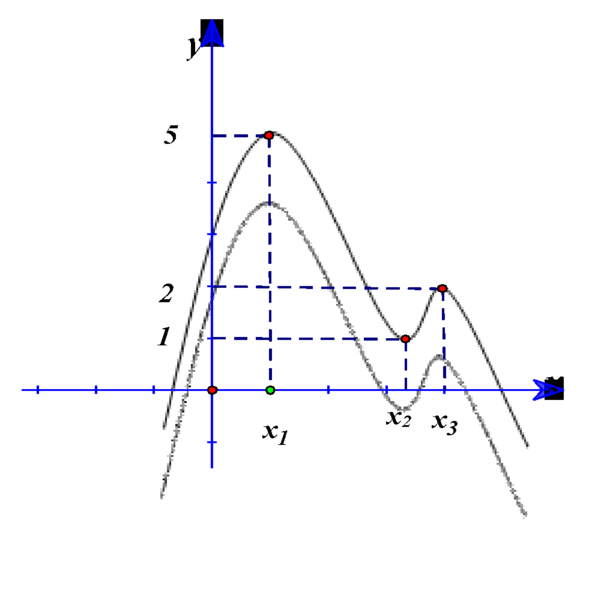
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi hàm số y = f f x + 2 có bao nhiêu điểm cực trị?
A. 12
B. 11
C. 9
D. 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 11 2018
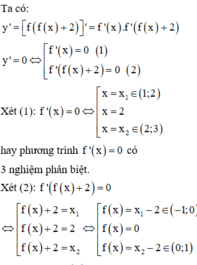
Chú ý: Một số em có thể sẽ quên mất khi xét số nghiệm của phương trình f(x) = 0 có 3 nghiệm phân biệt mà không loại nghiệm kép dẫn đến chọn nhầm đáp án C là sai.
CM
26 tháng 5 2018
Dựa vào đồ thị hàm số 
ta thấy hàm số có 3 điểm cực trị 
Xét hàm số
có
.
.
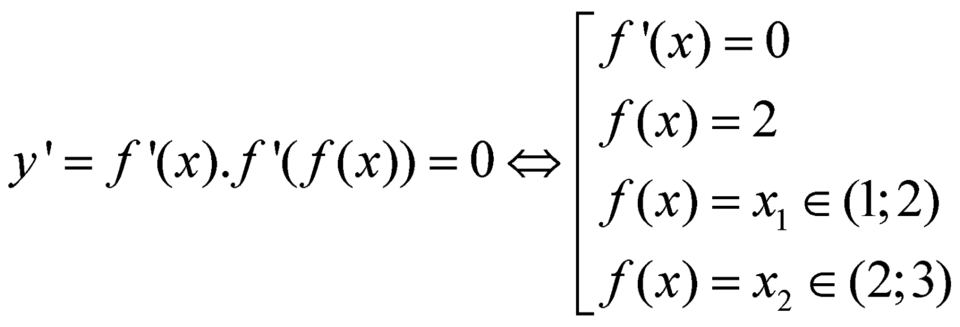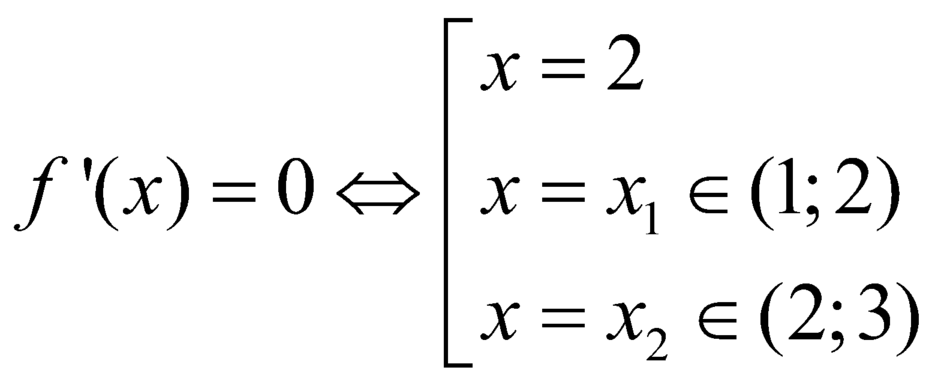Phương trình 
có 2 nghiệm đơn phân biệt.
Phương trình 
có 2 nghiệm đơn phân biệt.
Phương trình 
có 2 nghiệm đơn phân biệt.
Các nghiệm này không trùng nhau, do đó phương trình y’ = 0 có 9 nghiệm phân biệt (không trùng nhau),
Các nghiệm đều là nghiệm đơn. Do vậy hàm số 
có 9 điểm cực trị
Chọn D
CM
10 tháng 5 2019
Chọn D.
Phương pháp:
Xác định điểm trên đồ thị hàm số mà tại đó có đạo hàm đổi dấu.
Cách giải:
Quan sát đồ thị hàm số ta thấy, hàm số đạt cực trị tại 2 điểm x = 0, x = 1
CM
3 tháng 1 2020
Chọn D
Ta có
.
Suy ra đồ thị của hàm số y= g’(x) là phép tịnh tiến đồ thị hàm số y= f’(x) theo phương song song với trục Oy xuống dưới 
đơn vị.
Ta có 
và dựa vào đồ thị của hàm số y= f’(x) , ta suy ra
đồ thị của hàm số y= g’(x) cắt trục hoành tại 4 điểm.
=> Hàm số y= g( x) có 4 cực trị .
CM
9 tháng 2 2019
Ta có 
Suy ra đồ thị của hàm số g’ (x) là phép tịnh tiến đồ thị hàm số y= f’ (x) theo phương Oy xuống dưới 
đơn vị.
Ta có 
và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
Chọn D.
Dựa vào hình vẽ, ta thấy (1) có 3 nghiệm phân biệt; (2) có 2 nghiệm phân biệt; (3) có 3 nghiệm phân biệt và các nghiệm trên đều là nghiệm đơn hoặc bội lẻ
Vậy hàm số đã cho có 3 + 3 + 2 + 3 = 11 điểm cực trị. Chọn B