Cho tứ diện ABCD có A B ⊥ C D , A C ⊥ B D . Góc giữa hai vecto A D → và B C → là
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

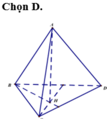


a) Có AD ⊥ AB( góc A vuông)
BC ⊥ AB( góc B vuông)
=> AD // BC
b) Có tứ giác ABCD= 360 độ
mà A = B= 90 độ
=> C + D= ABCD - A - B
= 360 độ - 90 độ - 90 độ
= 180 độ
Có D = 3C và C + D = 180 độ
=> C = 45 độ
=> D = 135 độ
c) Có ABCD= 360 độ
A = B= 90 độ
=> C + D= 180 độ
=> D =180 độ - C
+) D - C = 30 độ
<=> 180 độ - C - C = 30 độ
<=> 2C= 150 độ
<=> C = 75 độ
=> D = 105 độ
Vậy a) AD // BC
b) C = 45 độ
D = 135 độ
c) C = 75 độ
D = 105 độ

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Rightarrow30^0+70^0+\widehat{C}+\widehat{D}=360^0\)
\(\Rightarrow\widehat{C}+\widehat{D}=260^0\left(1\right)\)
Ta lại có: \(\widehat{C}-\widehat{D}=30^0\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\widehat{C}=145^0\)
\(\Rightarrow\widehat{D}=115^0\)

Ta có:
\(C-D=A-B\Rightarrow C-D-A+B=0\) (1)
\(A+B+C+D=360\)(2)
Cộng hai vế (1) và (2) ta có
\(C-D-A+B+A+B+C+D=0+360\)
\(\Leftrightarrow2B+2C=360\Leftrightarrow B+C=180\)(3)
\(A+B+C+D=360\Rightarrow A+B=360-\left(B+C\right)=360-180=180\)(4)
Từ (3)(4) suy ra ABCD LÀ HÌNH THANG ( Vì có 2 góc kề một cạnh bù nhau)

a, A + D = 110 + 70 = 180độ
=> AB // CD ( hai góc trong cùng phía bù nhau)
b, vì AB//CD => B +C = 180 độ
B: C = 7/3 => B /7 = C / 3 = (B+C) /(7+3) = 180 / 10 = 18 độ (Áp dụng dãy tỉ số bằng nhau)
=> B = 18 . 7 = 126độ

Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Rightarrow\widehat{C}+\widehat{D}=360^0-\widehat{A}-\widehat{B}=260^0\)
Mà \(\widehat{C}-\widehat{D}=40^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=\left(260^0+40^0\right):2=150^0\\\widehat{D}=\left(260^0-40^0\right):2=110^0\end{matrix}\right.\)

Tao có: \(\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{BC}\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CA}\)
\(=\frac{1}{2}\left(CB^2+CD^2-BD^2\right)-\frac{1}{2}\left(CB^2+CA^2-AB^2\right)\)
\(=\frac{1}{2}\left(AB^2+CD^2-BD^2-CA^2\right)\)
\(\Rightarrow\cos\left(\overrightarrow{BC},\overrightarrow{DA}\right)=\frac{1}{2}.\frac{c^2+c'^2-b^2-b'^2}{2aa'}\)

a) Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(Định lí tổng bốn góc trong một tứ giác)
mà \(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\dfrac{360^0}{10}=36^0\)
Do đó: \(\widehat{A}=36^0;\widehat{B}=72^0;\widehat{C}=108^0;\widehat{D}=144^0\)
Ta có: \(\widehat{B}+\widehat{C}=180^0\)
mà hai góc này là hai góc trong cùng phía
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)
hay ABCD là hình thang