Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,SA vuông góc với đáy. Biết S A = a , A B = a , B C = a 2 . Gọi I là trung điểm của BC. Cosin của góc giữa 2 đường thẳng A I v à S C là:
A. − 2 3
B. 2 3
C. a 3 3 6
D. a 3 3 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A.
Hướng dẫn giải: Gọi H là trung điểm của SB
⇒ IH song song với SC.
Do đó SC//(AHI)
![]()
Ta có A I = A B 2 + B I 2 = a 6 2
và I H = S C 2 = S A 2 + A C 2 2 = a
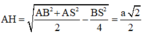
Áp dụng định lý cosin trong tam giác AHI, có
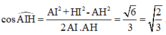

Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà

Đáp án B
Dựng hình bình hành AKCI khi đó S C ; A I ⏜ = S C ; C K ⏜
Ta có: A B = C K = A B 2 + B C 2 2 = a 6 2
S K = S A 2 + A K 2 = S A 2 + C I 2 = a 6 2
Khi đó cos S C K ⏜ = S C 2 + C K 2 − S K 2 2 S C . C K = 2 3 > 0 Do đó c os S C ; A I ⏜ = 2 3