Cho a là số thực dương khác 5. Tính I = log a 5 a 3 125
A. I = - 1 3
B. I = -3
C. I = 1 3
D. I = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 7 2019
Đúng(0)
Những câu hỏi liên quan
9 tháng 6 2018
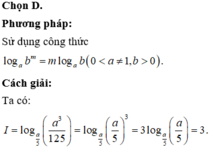
Bài 6 . Áp dụng BĐT Cauchy , ta có :
a2 + b2 ≥ 2ab ( a > 0 ; b > 0)
⇔ ( a + b)2 ≥ 4ab
⇔ \(\dfrac{\left(a+b\right)^2}{4}\)≥ ab
⇔ \(\dfrac{a+b}{4}\) ≥ \(\dfrac{ab}{a+b}\) ( 1 )
CMTT , ta cũng được : \(\dfrac{b+c}{4}\) ≥ \(\dfrac{bc}{b+c}\) ( 2) ; \(\dfrac{a+c}{4}\) ≥ \(\dfrac{ac}{a+c}\)( 3)
Cộng từng vế của ( 1 ; 2 ; 3 ) , Ta có :
\(\dfrac{a+b}{4}\) + \(\dfrac{b+c}{4}\) + \(\dfrac{a+c}{4}\) ≥ \(\dfrac{ab}{a+b}\) + \(\dfrac{bc}{b+c}\) + \(\dfrac{ac}{a+c}\)
⇔ \(\dfrac{a+b+c}{2}\) ≥ \(\dfrac{ab}{a+b}\) + \(\dfrac{bc}{b+c}\) + \(\dfrac{ac}{a+c}\)
9 tháng 6 2018
Bài 4.
Áp dụng BĐT Cauchy cho các số dương a , b, c , ta có :
\(1+\dfrac{a}{b}\) ≥ \(2\sqrt{\dfrac{a}{b}}\) ( a > 0 ; b > 0) ( 1)
\(1+\dfrac{b}{c}\) ≥ \(2\sqrt{\dfrac{b}{c}}\) ( b > 0 ; c > 0) ( 2)
\(1+\dfrac{c}{a}\) ≥ \(2\sqrt{\dfrac{c}{a}}\) ( a > 0 ; c > 0) ( 3)
Nhân từng vế của ( 1 ; 2 ; 3) , ta được :
\(\left(1+\dfrac{a}{b}\right)\left(1+\dfrac{b}{c}\right)\left(1+\dfrac{c}{a}\right)\) ≥ \(8\sqrt{\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{a}}=8\)
15 tháng 8 2023
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B
NT
2 tháng 3 2020
b) với mọi a,b,c ϵ R và x,y,z ≥ 0 có :
\(\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}\ge\frac{\left(a+b+c\right)^2}{x+y+z}\left(1\right)\)
Dấu ''='' xảy ra ⇔\(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}\)
Thật vậy với a,b∈ R và x,y ≥ 0 ta có:
\(\frac{a^2}{x}=\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}\left(2\right)\)
⇔\(\frac{a^2y}{xy}+\frac{b^2x}{xy}\ge\frac{\left(a+b\right)^2}{x+y}\)
⇔\(\frac{a^2y+b^2x}{xy}\ge\frac{\left(a+b\right)^2}{x+y}\)
⇔\(\frac{a^2y+b^2x}{xy}.\left(x+y\right)xy\ge\frac{\left(a+b\right)^2}{x+y}.\left(x+y\right)xy\)
⇔\(\left(a^2y+b^2x\right)\left(x+y\right)\ge\left(a+b\right)^2xy\)
⇔\(a^2xy+b^2x^2+a^2y^2+b^2xy\ge a^2xy+2abxy+b^2xy\)
⇔\(b^2x^2+a^2y^2-2abxy\ge0\)
⇔\(\left(bx-ay\right)^2\ge0\)(luôn đúng )
Áp dụng BĐT (2) có:
\(\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}\ge\frac{\left(a+b\right)^2}{x+y}+\frac{c^2}{z}=\frac{\left(a+b+c\right)^2}{x+y+z}\)
Dấu ''='' xảy ra ⇔\(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}\)
Ta có:
\(\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}
\)
= \(\frac{1}{a^2}.\frac{1}{ab+ac}+\frac{1}{b^2}.\frac{1}{bc+ac}+\frac{1}{c^2}.\frac{1}{ac+bc}\)
=\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ab}+\frac{\frac{1}{c^2}}{ac+bc}\)
Áp dụng BĐT (1) ta có:
\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ab}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{\left(\frac{1}{a}+\frac{1}{b}++\frac{1}{c}\right)^2}{2\left(ab+bc+ac\right)}\)
Mà abc=1⇒\(\left\{{}\begin{matrix}ab=\frac{1}{c}\\bc=\frac{1}{a}\\ac=\frac{1}{b}\end{matrix}\right.\)
\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ac}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}{2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)}\)
\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ac}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Có \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}=3\sqrt[3]{\frac{1}{1}}=3\)( BĐT cosi )
⇒\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\)
⇒\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ac}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{1}{2}.3=\frac{3}{2}\)
Vậy \(\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}\ge\frac{3}{2}\)
Chúc bạn học tốt !!!
19 tháng 12 2016
a) \(\frac{2}{3}+\frac{1}{3}:x=\frac{3}{5}\)
\(\frac{1}{3}:x=\frac{3}{5}-\frac{2}{3}=\frac{9}{15}-\frac{10}{15}=\frac{-1}{15}\)
\(x=\frac{-1}{15}.\frac{1}{3}\)
\(x=\frac{-1}{45}\)
Vậy x = \(\frac{-1}{45}\)
c) \(\left|2x-1\right|+1=4\)
\(\left|2x-1\right|=4-1=3\)
2x-1 = 3 ; -3
TH1: 2.x - 1 = 3
2.x = 3 + 1 = 4
x = 4 : 2 = 2
TH2: 2.x - 1 = -3
2.x = -3 + 1 = -2
x = -2 : 2 = -1
Vậy x \(\in\){ 2 ; -1 }
Ngại làm ấn máy ==
20 tháng 10 2017
Bài 1: Thực hiện phép tính:
a) 50 . 79 + 24 : 23 - 15
= 1 . 79 + 24 : 8 - 15
= 79 + 3 - 15
= 82 - 15
= 67.
b) 27 . 34 + 34 . 73
= (27 + 73) . 34
= 100 . 34
= 3400.
c) 43 . 46 + 54 . 43 - 120
= 43. (46 + 54) - 120
= 64 . 100 - 120
= 6400 - 120
= 6280.
d) 2 + 3 + 4 + ... + 69 + 70
= (70 + 2) . [(70 - 2) : 1 + 1] : 2
= 72 . 69 : 2
= 4968 : 2
= 2484.
Bài 2: Tìm số tự nhiên x, biết:
a) 5x = 25
\(\Rightarrow\) 5x = 52
\(\Rightarrow\) x = 2.
b) 3x + 2 = 81
3x . 32 = 81
\(\Rightarrow\) 3x . 32 = 34
\(\Rightarrow\) x + 2 = 4
x = 4 - 2
x = 2.
c) (x + 1)3 = 27
\(\Rightarrow\) (x + 1)3 = 33
\(\Rightarrow\) x + 1 = 3
x = 3 - 1
x = 2.
d) 6 : (2x - 1) + 45 = 490 . 47
6 : (2x - 1) + 45 = 1 . 47
6 : (2x - 1) + 45 = 47
6 : (2x - 1) = 47 - 45
6 : (2x - 1) = 2
2x - 1 = 6 : 2
2x - 1 = 3
2x = 3 + 1
2x = 4
x = 4 : 2
x = 2.
Bài 3: Tính:
a) 27 . 75 + 25 . 27 - 100
= 27 . (75 + 25) - 100
= 27 . 100 - 100
= 2700 - 100
= 2600.
b) 47 : 45 - 35 : 5 + 27 : 32
= 42 - 7 + 27 : 9
= 16 - 7 + 3
= 9 + 3
= 12.
c) 210 : 27 + 40030 . 29 - 135 : 45
= 23 + 1 . 29 - 135 : 45
= 8 + 29 - 3
= 37 - 3
= 34.
d) 12 : {390 : [500 - (125 + 35 . 7)]}
= 12 : {390 : [500 - (125 + 245)]
= 12 : {390 : [500 - 370]}
= 12 : {390 : 130}
= 12 : 3
= 4.
KL
20 tháng 3 2020
Bài 4:Nhìn rối quá,chưa hiểu
Bài 5:Bỏ dấu ngoặc rồi tính
1) ( 17 – 229) + ( 17 - 25 + 229)
=17-229+17-25+229
=17+17-229+229-25
=34-25=9
2)(125 – 679 + 145) – (125 – 679 )
=125-679+145-125+679
=125-(-125)+(-679)+679+145
=145
3)(3567 – 214) – 3567
=3567-214-3567
=-214
4)(- 2017) – ( 28 – 2017)
=-2017-28+2017
=-2017+2017-28
=-28
5) -( 269 – 357 ) + ( 269 – 357 )
=-269+357+269-357
=0
6) (123 + 345) + (456 – 123) – (45 – 144)
=123+345+456-123-45+144
=123-123+345+456-45+144
=0+345+456-45+144
=900 cái này mik tính gộp nha.Còn bn muốn tách thì tách nha
Bài 6*. Tìm số nguyên n để:
1) n + 3⋮ n + 1
Ta có: n + 3⋮ n + 1
⇔n+3=(n+1)+2
⇔(n+1)+2⋮n+1
⇔2⋮n+1
⇔n+1∈Ư(2)={-2;-1;1;2}
Ta có bảng sau
| n+1 | -2 | -1 | 1 | 2 |
| n | -3 | -2 | 0 | 1 |
Vậy n=-3;-2;0;1
2) 2n + 1⋮ n – 2
Ta có: 2n + 1⋮ n – 2
⇔2n+1=2n+0+1
⇔n+1∈Ư(1)={-1;1}
Ta có bảng sau:
| n+1 | -1 | 1 |
| n | -2 | 0 |
Vậy n=-2;0
3) (n - 2).(n + 3) < 0
Vì (n - 2).(n + 3) < 0
⇔n-2=n+3-1
⇔(n+3)-1.(n+3)<0
⇔1.n+3<0
⇔n+3∈Ư(1)={-1:1}
Ta có bảng sau:
| n+3 | -1 | 1 |
| n | -4 | -2 |
Vậy n là -4;-2
------Còn nữa------
P/s:Tại hơi mỏi tay
#Học tốt
KL
20 tháng 3 2020
Bn ơi,mai mốt bn chia ra từng câu cho dễ thấy nha,như vậy mấy bn khác đọc k ra sẽ k giúp bn đc