Cho a,b là các số thực dương. Mệnh đề nào dưới đây là đúng?
![]()
![]()
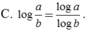
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu trắc nghiệm này kinh thật :D
\(P=\left(1+36abc\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+36\left(ab+bc+ca\right)\)
\(P=\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)+36\left(ab+bc+ca\right)\)
\(P=\dfrac{a^2+b^2}{ab}+\dfrac{b^2+c^2}{bc}+\dfrac{c^2+a^2}{ca}+3+36\left(ab+bc+ca\right)\)
\(P=\dfrac{\left(a+b\right)^2}{ab}+\dfrac{\left(b+c\right)^2}{bc}+\dfrac{\left(c+a\right)^2}{ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{\left(2a+2b+2c\right)^2}{ab+bc+ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{4}{ab+bc+ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge2\sqrt{\dfrac{144\left(ab+bc+ca\right)}{ab+bc+ca}}-3=21\)
Vậy \(P\ge21\)

Đáp án B
Ta có a 3 4 > a 4 3 ⇒ 0 < a < 1 ( d o 3 4 < 4 3 )
Mặt khác log b 1 2 < log b 2 3 ⇒ b > 1 ( d o 2 3 > 1 2 )