Cho a là số thực dương thỏa mãn a ≠ 10 , mệnh đề nào dưới đây sai?
K
Khách
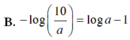
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 9 2018
Với mọi 0 < k ta có
a 2 + b 2 = 14 a b ⇒ a + b 2 = 16 a b ⇒ log k a + b 2 = log k 16 a b ⇒ 2 log k a + b 2 = log k 16 + log k a + log k b
Thử từng cơ số của k ta thấy đáp án D cho ra kết quả không chính xác
Đáp án D
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2020
Câu trắc nghiệm này kinh thật :D
\(P=\left(1+36abc\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+36\left(ab+bc+ca\right)\)
\(P=\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)+36\left(ab+bc+ca\right)\)
\(P=\dfrac{a^2+b^2}{ab}+\dfrac{b^2+c^2}{bc}+\dfrac{c^2+a^2}{ca}+3+36\left(ab+bc+ca\right)\)
\(P=\dfrac{\left(a+b\right)^2}{ab}+\dfrac{\left(b+c\right)^2}{bc}+\dfrac{\left(c+a\right)^2}{ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{\left(2a+2b+2c\right)^2}{ab+bc+ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge\dfrac{4}{ab+bc+ca}+36\left(ab+bc+ca\right)-3\)
\(P\ge2\sqrt{\dfrac{144\left(ab+bc+ca\right)}{ab+bc+ca}}-3=21\)
Vậy \(P\ge21\)
CM
9 tháng 4 2018
Đáp án B
Ta có a 3 4 > a 4 3 ⇒ 0 < a < 1 ( d o 3 4 < 4 3 )
Mặt khác log b 1 2 < log b 2 3 ⇒ b > 1 ( d o 2 3 > 1 2 )
Chọn B