Biết rằng parabol y = 1 24 x 2 chia hình phẳng giới hạn bởi elip có phương trình x 2 16 + y 2 1 = 1 thành hai phần có diện tích lần lượt là S1,S2với S1<S2. Tỉ số của S 1 S 2 bằng
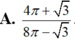
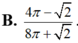
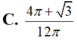

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
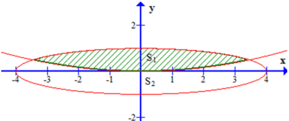
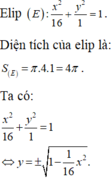
Nhận thấy S 1 là diện tích hình phẳng giới hạn bởi parabol y = 1 24 x 2 và phần elip nằm phía trên trục hoành.
Ta có phương trình hoành độ giao điểm của parabol y = 1 24 x 2 và elip x 2 16 + y 2 1 = 1 là
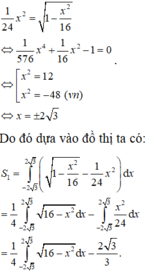
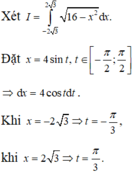
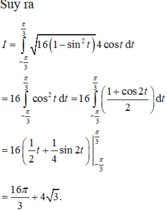
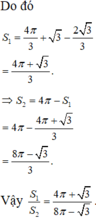

Chọn đáp án A
Phương trình hoành độ giao điểm của parabol y = 3 2 x 2 và nửa đường elip
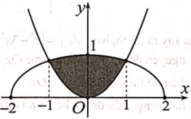
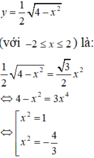
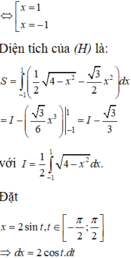
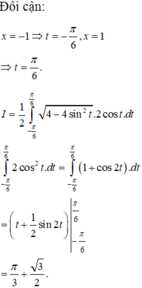
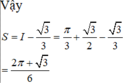

Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của 3 x 2 = 4 - x 2 <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2x ( ∫ 0 1 4 - x 2 d x - ∫ 0 1 3 x 2 d x ) = 2 π + 3 3

Đáp án B
Xét phương trình tương giao:
3 x 2 = 4 − x 2 ⇔ 3 x 4 = 4 − x 2 ⇔ x 2 = 1 ⇒ x = ± 1 x 2 = − 4 3 ( L ) S = ∫ 0 1 3 x 2 d x + ∫ 1 2 4 − x 2 d x = 3 x 3 3 1 0 + S 2 S 2 : x = 2 sin t , t ∈ ( − π 2 ; π 2 ) ⇒ d x = 2 cos t d t S 2 : ∫ π 6 π 2 2 cos t .2 cos t d t = ∫ π 6 π 2 4 cos 2 t d t = 2 ∫ π 6 π 2 ( 1 + cos 2 t ) d t = 2 [ t + sin 2 t 2 ] π 2 π 6 = 2 π 3 − 3 2 ⇒ S = 3 3 + 2 π 3 − 3 2
Đáp án A.