Tính diện tích toàn phần S t p của hình trụ tạo thành khi quay hình chữ nhật ABCD quanh cạnh AB, biết AB=5, BC=2
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

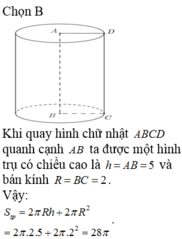

*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
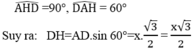
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
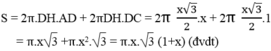
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = DC = 1, cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón
Ta có:
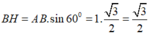
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
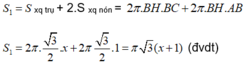

Đáp án C
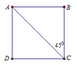
Vì ABCD là hình chữ nhật và A C B ⏜ = 45 ° nên ABCD là hình vuông.
Ta có: 2. A B 2 = 2 3 a 2 ⇔ A B = 6 a
S t p = 2 π B C 2 + 2 π . B C = 2 π . B C . A B = 2 π . 6 a 2 + 2 π . 6 a 2 = 24 π a 2