Cho số phức z thỏa mãn . Tìm giá trị lớn nhất của
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Đặt w = ( 1 + i)z , suy ra ![]()
Gọi M( x; y) là điểm biểu diễn của số phức w trên mặt phẳng Oxy.
Khi đó tập hợp điểm biểu diễn của số phức w là đường tròn tâm I(-1; 7) , bán kính ![]()
Ta có ![]()
Vậy 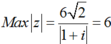

Tập hợp các điểm z thỏa mãn điều kiện z - 1 = 2 là đường tròn (C) tâm I(1;0) bán kính R = 2
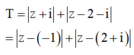
Gọi M là điểm biểu diễn cho số phức z, A(0,-1) là điểm biểu diễn cho số phức -i, B(2;1)là điểm biểu diễn cho số phức 2+i

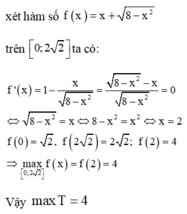
Đáp án D

Đáp án D
Phương pháp: Đưa biểu thức T về dạng biểu thức vector bằng cách tìm các vecto biểu diễn cho các số phức.
Cách giải:
Tập hợp các điểm z thỏa mãn điều kiện ![]() là đường tròn (C) tâm I(1;0) bán kính R=
2
là đường tròn (C) tâm I(1;0) bán kính R=
2
![]()
Gọi M là điểm biểu diễn cho số phức z, A(0;-1) là điểm biểu diễn cho số phức -i, B(2;1) là điểm biểu diễn cho số phức 2+i
Dễ thấy A,B
∈
C và ![]()
![]() AB là đường kính của đường tròn (C)
AB là đường kính của đường tròn (C)
![]() vuông tại M
vuông tại M
![]()
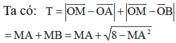
Đặt ![]()
Xét hàm số ![]() trên
trên ![]() ta có:
ta có:
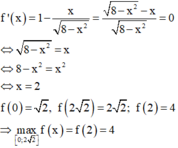
Vậy maxT=4

Chọn B.
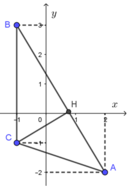
Gọi M (x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Gọi điểm A(2; -2) ; B(-1; 3) và C(-1; -1)
Phương trình đường thẳng AB: 5x + 3y - 4 = 0.
Khi đó theo đề bài ![]()
Ta có ![]() . Do đó quỹ tích M là đoạn thẳng AB.
. Do đó quỹ tích M là đoạn thẳng AB.
Tính CB = 4 và ![]() .
.
Hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.
Vậy 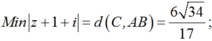
![]()
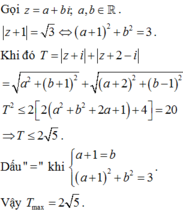
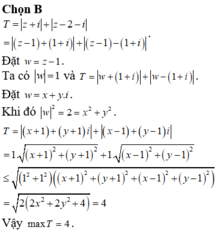

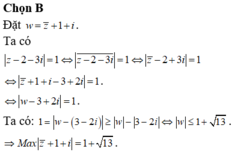
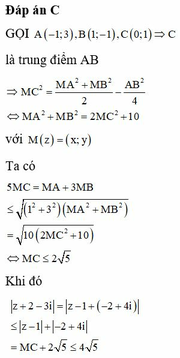
Chọn C.