Đồ thị hàm số đối xứng với đồ thị của hàm số qua điểm I (1;1).Giá trị của biểu thức là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(AB=\sqrt{\left(0-3\right)^2+\left(-3-0\right)^2}=3\sqrt{2}\)
\(C=OA+OB+AB=6+3\sqrt{2}\left(cm\right)\)

a) Để hàm số (1) đồng biến thì \(4-2a>0\Leftrightarrow-2a>-4\Leftrightarrow a< 2\)
b) Để đthị hàm số (1) song song với đt y=x-2 thì:
\(\left\{{}\begin{matrix}4-2a=1\\3-a\ne-2\end{matrix}\right.\) \(\Leftrightarrow a=\frac{3}{2}\)
c) Thay a=1 vào đthị hàm số (1) ta đc;
\(y=2x+2\)
Làm ra thì \(\left(-1,2\right)\)
Đồ thị tự vẽ nha.

Đáp án là B
Từ đồ thị của hàm số đã cho ta có:
Tiệm cận đứng của đồ thị hàm số là đường thằng có phương trình x = -1
Tiệm cận ngang của đồ thị hàm số là đường thằng có phương trình y = -1
Đồ thị hàm số đi qua các điểm (1;0) và (0;1)
Suy ra hàm số cần tìm là - x + 1 x + 1 .

Khi x= 2 thì y= - 0,5.2 = -1. Vậy điểm A(2; -1) thuộc đồ thị của hàm số y = f(x) = - 0,5x. Đồ thị của hàm số này là đường thẳng OA trong hình vẽ dưới đây:
O -1 -2 -3 1 2 2,5 3 -1 -2 -3 -4 -5 1 2 3 4 x y A
Trên đồ thị ta thấy:
a) f(2)= -1; f(-2)= 1; f(4)= -2; f(0)= 0.
b) y= -1 \(\Rightarrow\) x= 2;
y= 0 \(\Rightarrow\) x= 0;
y= 2,5 \(\Rightarrow\) x= -5.
c) y > 0 ứng với phần đồ thị phía trên trục hoành và ở bên trái trục tung nên x < 0.
y < 0 ứng với phần đồ thị nằm phía dưới trục hoành và ở bên trái trục tung nên a > 0.

Giao điểm với trục tung B(0 ;-1). Ta có
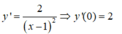
Hệ số góc của tiếp tuyến của đồ thị hàm số 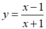 tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Chọn B

Đáp án A
Hệ số góc của tiếp tuyến của đồ thị hàm số chính là đạo hàm cấp 1
Ta có y = − x 3 − 3 x 2 + 2 ⇒ y ' = − 3 x 2 − 6 x ⇒ y ' ' = − 6 x − 6
Phương trình y ' ' = 0 ⇔ x = − 1
Vậy hệ số góc cần tìm là k = y ' 1 = 3
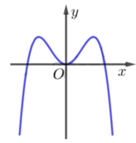

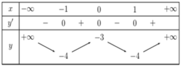

Đáp án là B