Viết phương trình mặt phẳng tiếp xúc với mặt cầu tại điểm M(6; -2; 3).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

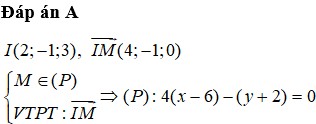
![]()

Đáp án A
Mặt cầu (S) có tâm I(-1;4;-3) và có bán kính R = 6. Gọi H là hình chiếu vuông góc của I trên trục Ox. Ta có H(-1;0;0) và IH=5.
Gọi K là hình chiếu vuông góc của I trên mặt phẳng (P). Ta có
d(I; (P)) = IK ≤ IH = 5 < R = 6
Do đó mặt phẳng (P) luôn cắt mặt cầu (S) theo một đường tròn. Vậy không tồn tại mặt phẳng (P) chứa Ox và tiếp xúc với (S)

Đáp án D
Mặt cầu (S) có tâm I(1;2;3).
Gọi (α) là mặt phẳng cần tìm. Do (α) tiếp xúc với (S) tại P nên mặt phẳng (α) đi qua P và có véc-tơ pháp tuyến ![]()
Phương trình mặt phẳng (α) là:
-6(x+5)-6(y+4)+3(z-6) = 0 <=> 2x + 2y - z + 24 = 0.

Đáp án B
Pt pháp tuyến của mặt phẳng cần tìm là n ⇀ = d , ⇀ ∆ ⇀ = (1;0;1)
Pt có dạng: x+z+D=0
Khoảng cách từ O (-1;1;-2) đến mp là 2
⇒ D=1
Pt có dạng : x+z+1=0

Lời giải:
Bán kính mặt cầu là:
\(R=d(M, (a))=\frac{|1-1-2(-2)-2|}{\sqrt{1^2+1^2+2^2}}=\frac{\sqrt{6}}{3}\)
PT mặt cầu $(S)$ là:
$(x-1)^2+(y-1)^2+(z+2)^2=\frac{2}{3}$





