Kết quả của phép tính ∫ d x e x - 2 e - x + 1 bằng:
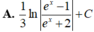
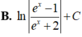
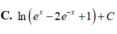
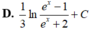
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, (1 999 + 2 378 + 4 545 + 7 956) – (315 + 598 + 736 + 89)
=1 999 + 2 378 + 4 545 + 7 956 – 315 - 598 - 736 - 89
= ( 1999 - 89 ) + ( 2 378 - 598 ) + ( 4 545 - 315 ) + ( 7 956 - 736 )
= ......0 + ........0 + .........0 + .......0
= ........0 có chữ số tận cùng là 0

Phần a là 0
Phần b là 5
Phần c là 6
Phần d là 1
Phần e là 0

hì hì câu a mk ko làm được.
b) ta áp dụng bất kì tích nào có thừa số 5 thì tích đó sẽ có chữ số tận cùng là 5.
c) ta áp dụng tính chất chữ số tận cùng của thừa số là 6. 6 nhân bất kì số nào thì có cữ số tận cùng không nhất định.nhưng 6 nhân 6 thì luôn luôn có chữ số tận cùng là 6.
d) dễ rồi 1 nhân với 1 chắc chắn sẽ bằng 1 nên chữ số tận cùng là 1.
e) ta chia thành 2 vế. vế a(56x66x76x86) - vế b(51x61x71x81)
*ta xét vế a. như câu c ta có chữ số tận cùng là 6.
*ta xét vế b tương tự như câu d có chữ số tận cùng là 1.
vậy a-b=6-1=5. vậy có chữ số tận cùng là 5
tk nha

\(\begin{array}{l}f'(x) = \mathop {\lim }\limits_{x \to 0} \frac{{f(x + {x_0}) - f(x)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{x + {x_0}}} - {e^x}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{x + {x_0}}} - {e^x}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to 0} \frac{{{e^x}({e^{{x_0}}} - 1)}}{x} = {e^x}.\mathop {\lim }\limits_{x \to 0} \frac{{{e^{{x_0}}} - 1}}{x} = {e^x}.1 = {e^x}\\ \Rightarrow f'(x) = {e^x}\end{array}\)

\(a,3^6\cdot3^7=3^{6+7}=3^{13}\)
\(b,5\cdot5^4\cdot5^2\cdot5^5=5^{1+4+2+5}=5^{12}\)
\(c,a^4\cdot a^5\cdot a^{10}=a^{4+5+10}=a^{19}\)
\(d,x^{10}\cdot x^4\cdot x=x^{10+4+1}=x^{15}\)
\(e,3\cdot3\cdot3\cdot9=3^3\cdot3^2=3^5\)
\(f,a^2\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a=a^{2+1+1+1+1+1+1}=a^8\)
a: 3^6*3^7=3^13
b: \(=5^{1+4+2+5}=5^{11}\)
c: \(=a^{4+5+10}=a^{19}\)
d: \(=x^{10+4+1}=x^{15}\)
e: \(=3^3\cdot3^2=3^5\)
f: \(=a^2\cdot a^6=a^8\)
Chọn B