Trong các số phức: (1+i)2, (1+i)8, (1+i)3, (1+i)5 số phức nào là số thực? A. (1+i)3 B. (1+i)8 C. (1+i)2...
Đọc tiếp
Trong các số phức: (1+i)2, (1+i)8, (1+i)3, (1+i)5 số phức nào là số thực?
A. (1+i)3
B. (1+i)8
C. (1+i)2
D. (1+i)5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 2 2019
Đáp án B
Phương pháp:
Sử dụng 
Cách giải:
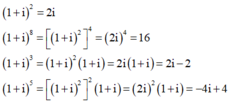
Như vậy, chỉ có số phức 
là số thực
CM
7 tháng 3 2019
Chọn A.
Ta có: (1 + i) 2( 2 - i) z = 8 + i + (1 + 2i) z.
Suy ra: (2 + 4i)z - (1 + 2i)z = 8 = i
Vậy phần thực của z bằng 2.
CM
26 tháng 10 2017
Chọn A. Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó:
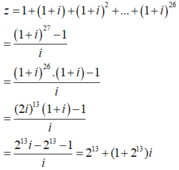
Vậy phần thực là: 213
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 5 2020
a/\(\left(1+i\right)z=\frac{1}{z}\Leftrightarrow z^2\left(1+i\right)=1\Rightarrow z^2=\frac{1}{1+i}=\frac{1}{2}-\frac{1}{2}i\)
\(\Rightarrow\) Phần ảo là \(-\frac{1}{2}\)
b/\(\frac{1}{z}=\frac{1}{2}+\frac{1}{2}i\Rightarrow z=\frac{2}{1+i}\Rightarrow z=1-i\)
Phần ảo là -1
c/ Áp dụng công thức tổng CSN với \(u_1=i\) ; \(q=i\); \(n=100\)
\(i+i^2+...+i^{100}=i.\frac{i^{101}-1}{i-1}=\frac{i^{102}-i}{i-1}=\frac{\left(i^2\right)^{51}-i}{i-1}=\frac{-1-i}{i-1}=i\)
d/ Tương tự câu trên:
\(1+\left(1+i\right)+...+\left(1+i\right)^{20}=1+\left(1+i\right).\frac{\left(1+i\right)^{21}-1}{1+i-1}=-2048+i\)
CM
31 tháng 12 2018
Chọn C.
Ta có: ( 1 + i)2(2 - i) z = 8 + i + (1 + 2i)z
Nên z[( 1 + i)2(2 -i) – (1 + 2i) ] = 8 + i
Suy ra: z[2i(2 - i) – 1 - 2i] = 8 + i
Vậy số phức z đã cho có phần thực là 2, phần ảo là -3.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
\(\Leftrightarrow\left(1-2i\right)z-\left(\dfrac{1}{2}-\dfrac{3}{2}i\right)=\left(3-i\right)z\)
\(\Leftrightarrow\left(1-2i\right)z-\left(3-i\right)z=\dfrac{1}{2}-\dfrac{3}{2}i\)
\(\Leftrightarrow\left(-2-i\right)z=\dfrac{1}{2}-\dfrac{3}{2}i\)
\(\Rightarrow z=\dfrac{1-3i}{2\left(-2-i\right)}=\dfrac{1}{10}+\dfrac{7}{10}i\)
\(\Rightarrow A\left(\dfrac{1}{10};\dfrac{7}{10}\right)\) \(\Rightarrow\) tọa độ trung điểm I là \(\left(\dfrac{1}{20};\dfrac{7}{20}\right)\)
Đáp án B
Phương pháp: Sử dụng (1+i)2 = 1+2i+i2 = 1+2i – 1 = 2i
Cách giải:
Như vậy, chỉ có số phức (1+i)8 là số thực