Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
f x g x = h x = c g x g x ≠ 0 với c là hằng số
Gọi điểm x 0 ; y 0 x 0 ; y 0 ∈ ℤ là các điểm thuộc đồ thị hàm số cần tìm.
Ta có
y 0 = x 0 − 1 x 0 + 1 = x 0 + 1 − 2 x 0 + 1 = 1 − 2 x 0 + 1 ∈ ℤ ⇔ x 0 + 1 ∈ U 2 = ± 1 ; ± 2
Ta có bảng giá trị sau:
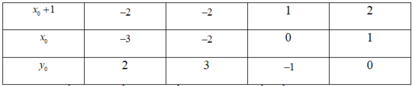
Vậy có 4 điểm thuộc đồ thị hàm số thỏa mãn yêu cầu đề bài.
Đáp án A
Ta có: 
Giả sử 
là 1 điểm thuộc (C) có tọa độ nguyên
Suy ra 
là ước của 2. Do đó: 
a) Để đồ thị hàm số y = 3x + 1 đi qua A có hoành độ bằng \(\dfrac{2}{3}\) thì :
=> \(y=3\cdot\dfrac{2}{3}+1=3\)
Vậy tung độ của điểm A là 3
b) Với x nguyên dương :
\(P=\dfrac{\left|x+5\right|+6}{\left|x+5\right|+4}=\dfrac{x+5+6}{x+5+4}=\dfrac{x+11}{x+9}=\dfrac{x+9+2}{x+9}=1+\dfrac{2}{x+9}\)
Để P max <=> \(\dfrac{2}{x+9}max\Leftrightarrow x+9\) min <=> x min
Mà x là số nguyên dương <=> x = 1
Vậy MaxP = \(1+\dfrac{2}{1+9}=\dfrac{6}{5}\Leftrightarrow x=1\)
Gọi tung đọ của A là x
hoành độ của A là y
theo bài ra ta có y= 3x +1
=> y= 3\(\dfrac{2}{3}+1\)
=> y= 2 +1
=> y= 3
vậy tung độ của A là 3
b, x là \(\dfrac{2}{3}\)
=> P = (/ \(\dfrac{\left(\dfrac{2}{3}+5\right)+6}{\left(\dfrac{2}{3}+5\right)+4}\)
=> P =\(\dfrac{35}{39}\)
Do tiếp tuyến tại cắt trục tọa độ Ox, Oy lần lượt tại A, B nên tiếp tuyến có hệ số góc k với 
Ta có 
nên k = -3
Khi đó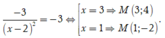 
Chọn B.
Chọn D