Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a, điểm K thuộc cạnh SC sao cho SK=2KC. Mặt phẳng (P) chứa AK và song song BD. Tính diện tích của thiết diện của hình chóp S.ABCD cắt bởi (P).
A. 3 a 2 5
B. 2 26 a 2 15
C. 4 26 a 2 15
D. 2 3 a 2 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
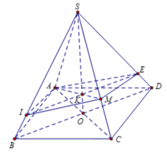
Vì P / / B D nên P ∩ S B D = I E / / B D
Ta có B D ⊥ S O , B D ⊥ A C ⇒ B D ⊥ S A C ⇒ B D ⊥ A M
⇒ I E ⊥ A M
Ta có S M M C . A C A O . O K K S = 1 ⇔ 2.2. O K K S = 1 ⇔ O K K S = 1 4
S M M C . I E B D = S K S O = 4 5 ⇒ I E = 4 5 B D = 4 a 2 5
Vì A C 2 = S A 2 + S C 2 nên Δ S A C vuông tại S
S M = 2 3 a ; A M = a 2 + 2 3 a 2 = a 13 3
S A E M I = 1 2 E I . A M = 1 2 . 4 a 2 5 . a 13 3 = 2 26 a 2 15

Kẻ SO vuông góc (ABCD)
\(AM\subset\left(P\right)\)trong mp(SAC)
Gọi AM giao SD=I
Trong mp(SBD) qua I kẻ đường song song với BD cắt SB tại F, cắt SD tại E
=>Thiết diện cần tìm là tứ giác AEMF

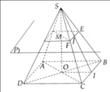
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).