Cho tam giác vuông cân ABC với AB=AC=a Khi quay tam giác đó (cùng với phần trong của nó) quanh đường thẳng đi qua B và song song với AC, ta được khối tròn có thể tích bằng
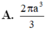
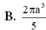
![]()
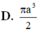
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
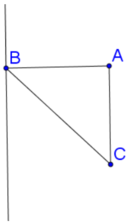
Thể tích khối tròn thu được bằng hiệu thể tích hình trụ bán kính đáy AB chiều cao AC trừ cho thể tích nón đỉnh B bán kính đáy AB chiều cao AC
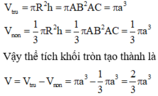

Đáp án A
Công thức thể tích khối nón V n o n = 1 3 π R 2 h ;
Ở đây R = O C .
Ta có 1 O C 2 = 1 C A 2 + 1 C B 2 = 1 a 2 + 1 b 2 = a 2 + b 2 a 2 b 2 ⇒ O C = a b a 2 + b 2 = R
Thể tích khối tròn xoay cần tính
V = 1 3 π O C 2 . O B + 1 3 π O C 2 . O A = 1 3 π R 2 . A B = 1 3 π a 2 b 2 a 2 + b 2 . a 2 + b 2 = π 3 . a 2 b 2 a 2 + b 2

Chọn C.
Phương pháp:
Dựng hình, xác định các hình tròn xoay tạo thành khi quay và tính tỉ số thể tích.
Cách giải:
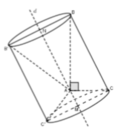
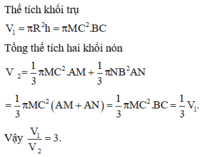

Thể tích của hình tròn xoay được tạo ra bằng thể tích của hình trụ có \(R=h=a\) trừ thể tích hình nón có \(R=a;h=a;l=a\sqrt{2}\)
\(\Rightarrow V=\pi.R^2h-\frac{1}{3}\pi R^2h=\frac{2}{3}\pi R^2h=\frac{2}{3}\pi a^3\)

Đáp án B
Gọi H là hình chiếu của C trên AB. Khi quay quanh AB ta sẽ thu được một hình nón bị thiếu đáy và thể tích phần đáy bị thiếu lại chính bằng thể tích của khối nón nhỏ khi quay ∆ A B C quanh AH. Vậy thể tích cần tính là
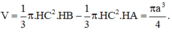
Chọn A
Thể tích khối tròn thu được bằng hiệu thể tích hình trụ bán kính đáy AB chiều cao AC trừ cho thể tích nón đỉnh B bán kính đáy AB chiều cao AC