Cho f(x) có tập xác định là
ℝ
và
f
'
(
x
)
=
x
-
1
x
4
. Chọn kết luận đúng. ...
Đọc tiếp
Cho f(x) có tập xác định là ℝ và f ' ( x ) = x - 1 x 4 . Chọn kết luận đúng.
K
Khách
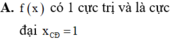
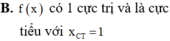
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 6 2019
Đáp án D
Dựa vào bảng biến thiên, ta có lim x → 1 y = ± ∞ ⇒ x = − 1 là TCĐ của đồ thị hàm số
Và lim x → ± ∞ y = + ∞ suy ra hàm số không có tiệm cận ngang
CM
5 tháng 1 2020
Đáp án C.
Ta có f x = ∫ f ' x d x = ∫ 1 x 2 - 1 d x = 1 2 ln x - 1 x + 1 + C .
· Với [ x > 1 x < - 1 ⇒ f x = 1 2 ln x - 1 x + 1 + C mà f - 3 + f 3 = 0 ⇒ 2 C + 1 2 ln 1 2 + 1 2 ln 2 = 0 ⇔ C = 0 .
· Với - 1 < x < 1 ⇒ f x = 1 2 ln 1 - x x + 1 + C mà f - 1 2 + f 1 2 = 2 ⇒ 2 C + 1 2 ln 1 3 + 1 2 ln 3 = 2 ⇔ C = 1 .
Vậy T = f - 2 + f 0 + f 4 = 1 2 ln - 2 - 1 - 2 + 1 + 1 2 ln 1 - 0 0 + 1 + 1 + 1 2 ln 4 - 1 4 + 1 = 1 + 1 2 ln 9 5 .
CM
23 tháng 12 2017
Chọn C
Hàm số f(x) =
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
ℝ
Vì m nguyên nên 
Vậy có tất cả 7 giá trị m thỏa mãn điều kiện đề bài.
CM
5 tháng 12 2019
Đáp án D
(2) sai vì xảy ra trường hợp x 0 không thuộc K . Ví dụ hàm
PT
0
Chọn C